A transformação isocórica é um processo termodinâmico onde gases, em um sistema fechado, sofrem alteração de pressão e temperatura, porém o volume é constante. É um fenômeno presente no cotidiano em latas de desodorantes aerossóis, por exemplo. Saiba mais sobre esse processo, veja os gráficos de uma função isocórica e alguns exemplos do fenômeno aplicado ao dia-a-dia.
Publicidade
O que é uma transformação isocórica
Também conhecida como transformação isovolumétrica, a transformação isocórica é um processo termodinâmico em que gases, confinados em sistemas fechados, sofrem algum tipo de alteração em pressão e temperatura, mas mantêm seu volume constante. O nome do processo é derivado das palavras gregas “isos” (igual) e “khóra” (espaço, volume).
Relacionadas
Foi estudada independentemente por dois cientistas franceses, Jacques Alexandre César Charles e Joseph Louis Gay-Lussac, que acabaram chegando às mesmas conclusões, propondo a Lei de Charles-Gay-Lussac: “Para uma certa massa fixa de gás, com seu volume constante, sua pressão é diretamente proporcional à sua temperatura.”
A alteração de pressão no sistema será diretamente proporcional à mudança de temperatura, ou seja, se determinado gás sofre um aquecimento em que sua temperatura passe a ser o dobro da inicial, sua pressão final também será duplicada. O mesmo acontece para o resfriamento do gás, porém nesse caso a pressão diminui na mesma proporção que a temperatura abaixa. Veja abaixo alguns exemplos da transformação isocórica.
Exemplos
- Lata de desodorante aerossol: as latas de desodorantes são recipientes rígidos e, consequentemente, de volume constante. Caso ela seja aquecida, o gás contido dentro dela sofre um aumento de temperatura e de pressão, causando risco de explosão da lata, por isso existe o aviso nos rótulos das embalagens de desodorante de não armazenar em lugares de elevada temperatura.
- Pneu de carro: considerando que os pneus de um carro possuam um caráter inelástico, ou seja, de volume constante, durante uma viagem eles se aquecem devido ao atrito com a estrada. Isso faz com que sua temperatura interna aumente. Sendo assim, ao final do percurso, é possível perceber que a calibragem do pneu mostra um valor maior que no início, justamente por conta da transformação isocórica que aconteceu.
Nesse sentido, é importante salientar que não se deve calibrar pneus de carros com pressões muito altas. Conforme o aquecimento durante uma viagem, corre o risco de estourar o pneu com o aumento da pressão interna. É preciso verificar qual a pressão ideal de calibragem de cada pneu nas diferentes situações de trânsito.
Equação para expressar a transformação isocórica
Nesse processo em que o volume é mantido constante e há variação em pressão e temperatura, a relação pode ser expressa matematicamente da seguinte maneira:
Publicidade
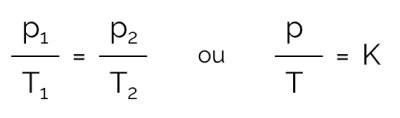
Em que:
- p: pressão (em Pa ou atm)
- T: temperatura (em Kelvin)
- K: constante
Note que a pressão e temperatura devem ser diretamente proporcionais, ou seja, na medida que uma aumenta, a outra também sofre a alteração com a mesma intensidade. Além disso, a relação entre p/T é sempre constante. Portanto, é possível observar graficamente o processo, como mostrado no tópico seguinte.
Publicidade
Gráfico de uma função isocórica
Tendo em vista que a equação matemática que determina uma transformação isocórica é uma função linear, ou seja, do tipo f(x) = ax, o gráfico obtido é uma reta. Isso comprova a proporcionalidade entre as grandezas avaliadas. Veja abaixo o gráfico da relação entre pressão x temperatura e do gráfico da relação de pressão x volume.
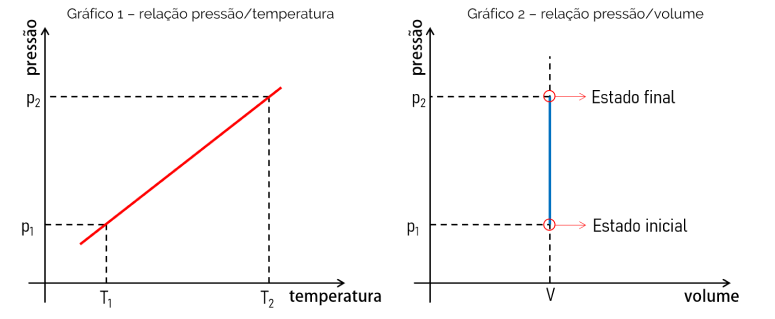
O gráfico 1 mostra a relação pressão x temperatura. Essa relação é linear e o gráfico é uma linha reta onde o coeficiente angular dela será igual ao valor da razão entre p e T. Já o gráfico 2, comprova que em uma transformação isocórica, o volume não se altera com o aumento da pressão, por exemplo.
Entender graficamente como ocorre esse processo termodinâmico é importante para a resolução de exercícios. A transformação isocórica pode se unir com as demais transformações gasosas, tornando o estudo da termodinâmica essencial para vestibulares e provas como o ENEM.
Vídeos sobre a transformação isovolumétrica
Veja abaixo alguns vídeos que foram selecionados para ajudar a assimilar o conteúdo estudado:
Entendendo a transformação isocórica
Entre as transformações gasosas, a transformação isocórica é aquela em que o volume é mantido constante, portanto pode ser chamada também de “isovolumétrica”. Para descrever esse fenômeno a Lei de Charles-Gay-Lussac, ou apenas Lei de Charles, é utilizada. Ela relaciona as pressões e temperaturas iniciais com as finais de um sistema termodinâmico. Assista ao vídeo para saber mais sobre essa lei e entenda a equação e o gráfico da transformação.
Transformação isovolumétrica na prática
Um dos exemplos mais comuns apresentados em livros didáticos sobre a transformação isocórica é a da calibragem dos pneus de carros. Ao andar com o veículo, a temperatura dos pneus aumenta por conta do atrito com o asfalto. E quando ela aumenta, é necessário aliviar um pouco dessa pressão, que também aumentou, para não estourar o pneu. Nesse vídeo, veja como aplicar os conhecimentos acerca desse conteúdo.
Exercícios resolvidos sobre a transformação isocórica
Esse tópico é muito cobrado em provas e vestibulares e pode causar confusões com qual grandeza é mantida constante nas resoluções dos exercícios. Para não se confundir mais, nada melhor que praticar o conteúdo resolvendo exercícios reais. Veja a explicação de alguns exercícios de vestibulares sobre a transformação isocórica.
Em síntese, a transformação isocórica acontece quando há uma mudança de temperatura e pressão em mesma intensidade em sistemas gasosos, porém o volume é mantido constante. Não pare de estudar por aqui, saiba mais sobre a lei dos gases, que envolve os três tipos de processos termodinâmicos de sistemas gasosos.
Referências
Fundamentos de física – volume 2 (1970) – David Halliday, Robert Resnick e Jearl Walker
Fundamentos de Físico-Química (1986) – Gilbert Castellan
Princípios de Química: Questionando a Vida Moderna e o Meio Ambiente (2005) – Peter Atkins e Loretta Jones

Por Lucas Makoto Tanaka dos Santos
Bacharel em Química pela Universidade Estadual de Maringá (UEM), mestrando em Química Analítica, com ênfase em desenvolvimento de métodos analíticos, metabolômica e espectrometria de massas no Laboratório de Biomoléculas e Espectrometria de Massas (LaBioMass), na mesma universidade.
Tanaka dos Santos, Lucas Makoto. Transformação isocórica. Todo Estudo. Disponível em: https://www.todoestudo.com.br/quimica/transformacao-isocorica. Acesso em: 24 de April de 2025.
1. [MACK-SP]
Uma determinada massa fixa de gás contido em um balão encontra-se inicialmente em CNTP. Em uma transformação isovolumétrica, sabendo-se que a pressão máxima interna permitida pelo balão é de 3,0 atm, se dobrarmos a temperatura absoluta inicial, a pressão final do gás e o efeito sobre o balão serão:
a) 2,0 atm e o balão não estoura
b) 2,0 atm e o balão estoura
c) 3,0 atm e o balão estoura
d) 1,5 atm e o balão não estoura
e) 1,0 atm e o balão não estoura
Considerando que a transformação que ocorre é do tipo isovolumétrica, ou seja, isocórica, a equação utilizada é a da lei de Charles-Gay-Lussac. As condições iniciais são em CNTP, isso significa que a temperatura é de 273 K (0°C) e a pressão é de 1 atm.
Os dados são, então:
p1 = 1 atm
T1 = 273 K
p2 = ?
T2 = 2 x T1 = 2 x 273 = 546 K
Sendo assim:
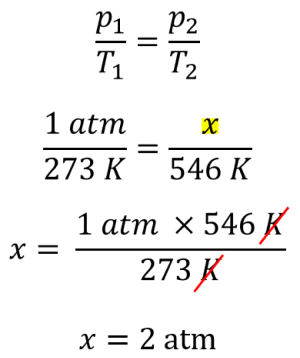
A alternativa correta é a letra a) 2,0 atm e o balão não estoura, porque o limite de pressão que o balão suporta é de 3 atm. Como não chega a essa pressão, ele não estoura.
2. [PUC-RJ]
Um pneu de bicicleta é calibrado a uma pressão de 4 atm, em um dia frio, à temperatura de 7 °C. O volume e a quantidade de gás injetado são os mesmos. Qual será a pressão de calibração no pneu quando a temperatura atinge 37 °C?
a) 21,1 atm
b) 4,4 atm
c) 0,9 atm
d) 760 mmHg
e) 2,2 atm
Antes de mais nada, para que o resultado seja correto, é preciso converter a temperatura em Celsius para Kelvin somando o valor de 273 às temperaturas em °C. Portanto, os dados fornecidos pelo exercício são:
p1 = 4 atm
T1 = (7 + 273) = 280 K
p2 = ?
T2 = (37 + 273) = 310 K
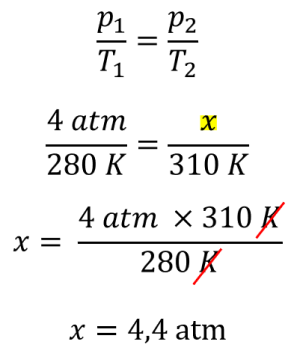
Então a alternativa correta é a letra b) 4,4 atm