Trigonometria

De origem grega, o termo trigonometria significa “medida das partes de um triângulo” e é um ramo da Matemática que se ocupa do estudo das relações entre os comprimentos de 2 lados de um triângulo retângulo.

Publicidade

Os conceitos referentes à trigonometria e funções trigonométricas podem ser aplicados na astronomia, sistemas de navegação, teoria musical, eletrônica, estatística, biologia, meteorologia e muitos outros campos de interesse da humanidade.

História da Trigonometria

Apesar de a palavra ter origem grega, o conceito da medida de ângulo ainda provoca debates, uma vez que não se sabe exatamente se surgiu com os gregos ou se eles, devido ao contato com a civilização babilônica, adotaram as suas frações sexagesimais. No entanto, pode-se afirmar que os gregos foram responsáveis por realizarem um estudo sistemático das relações entre ângulos numa circunferência e os comprimentos de suas cordas.

Na segunda metade do século II a.C., o astrônomo Hiparco de Nicéia foi o responsável por construir o que deve ter sido a primeira tabela trigonométrica da história, e por esta façanha, passou a ser chamado de “o pai da Trigonometria”.
Por volta de 100 d.C., o matemático grego Menelau de Alexandria produziu um tratado sobre cordas num círculo. Já a obra “Syntaxis mathematica”, escrita por Ptolomeu de Alexandria, é considerada a mais influente obra trigonométrica da Antiguidade.

Durante o século XVIII, vários estudos acerca das funções trigonométricas de uma variável complexa foram realizados.

A Trigonometria no triângulo retângulo

Define-se triângulo como sendo uma figura geométrica plana, formada por três lados e três ângulos internos. Tais ângulos são medidos na unidade de medida conhecida como grau e, cada um deles mede entre 0º e 180º. Em qualquer triangula, a soma dessas medidas deve ser igual a 180º. O triângulo retângulo é aquele onde um dos ângulos é reto, isto é, mede 90º, e os outros dois ângulos são agudos.

Em um triângulo retângulo são definidas as razões trigonométricas, isto é, as relações entre os lados do triângulo. É preciso ter em mente que o maior lado em um triângulo qualquer é sempre o lado oposto ao maior ângulo e, devido a soma dos ângulos de um triângulo ser 180º, o maior ângulo em um triângulo retângulo é o ângulo reto. Consequentemente, o maior lado nesse triângulo é o lado oposto ao ângulo reto, chamado de hipotenusa e os demais lados são denominados catetos.
Observe o triângulo retângulo a seguir:

Publicidade

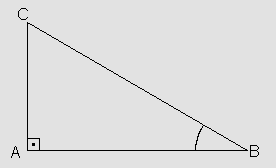
Neste exemplo, vamos considerar o ângulo que tem vértice em B, cuja medida x, em graus, é um número real que está no intervalo ]0,90[. Considerando a relação entre os lados do triângulo, pode-se estabelecer as seguintes razões:

• Seno – Seno de x é a razão entre o comprimento do cateto oposto ao ângulo B e o comprimento da hipotenusa do triângulo. Podemos indicar que Sen x = AC/BC.
• Cosseno – Cosseno de x é a razão entre o comprimento do cateto adjacente ao ângulo e o comprimento da hipotenusa do triângulo. Podemos indicar que Cos x = AB/BC.
• Tangente – Tangente de x é a razão entre os comprimentos do cateto oposto e do cateto adjacente ao ângulo B. Podemos indicar que Tg x = AC/AB.

Círculo Trigonométrico

O Círculo Trigonométrico foi criado para facilitar a visualização das proporções entre os lados dos triângulos retângulos. Este recurso consiste em uma circunferência orientada de raio unitário, centrada na origem dos 2 eixos de um plano cartesiano ortogonal.

Dados dois pontos A e B numa circunferência, pode-se sair de A e chegar em B andando pelo sentido anti-horário; no sentido horário; andando no sentido anti-horário, dando algumas voltas na circunferência e parando em B; e andando no sentido horário, dando algumas voltas na circunferência e parando em B. Adotou-se, por convenção, que o sentido anti-horário é positivo, enquanto o sentido horário é o negativo.

Publicidade

Referências