No estudo da geometria, podemos dizer que o triângulo é uma das mais importantes formas geométricas, sendo bastante usado na prática, principalmente em construções. A partir dessa simples figura geométrica, podemos obter diversas relações importantes, como é o caso do Teorema de Pitágoras, por exemplo, uma das mais famosas relações envolvendo os triângulos.
Publicidade
O triângulo nada mais é do que um polígono que, inclusive, é o que menos lados possui, sendo apenas 3. A soma dos ângulos internos dos triângulos sempre será igual a 180°, independentemente de qual seja a sua classificação. Os triângulos são classificados a partir das medidas dos lados, assim como a medidas dos ângulos internos que possuem.
Classificação dos triângulos
Como mencionado anteriormente, os triângulos podem ser classificados a partir das medidas de seus ângulos, ou ainda pela quantidade de lado que possuem. Quanto aos lados, a classificação pode ser da seguinte maneira:
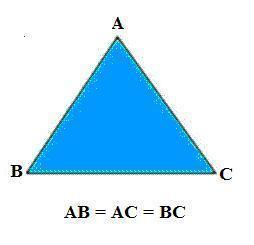
Triângulo equilátero: são os triângulos que apresentam os três lados com a mesma medida, ou seja, congruentes, como demonstrado na imagem abaixo.
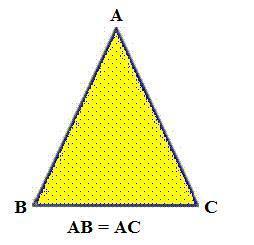
Triângulo isósceles: são aqueles que possuem dois lados com a mesma medida.
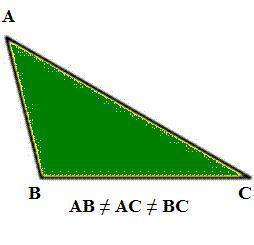
Triângulo escaleno: são aqueles que possuem medidas diferentes em seus três lados.
A classificação também pode ser feita com base nos ângulos internos, podendo ser acutângulo, retângulo ou obtusângulo.
Publicidade
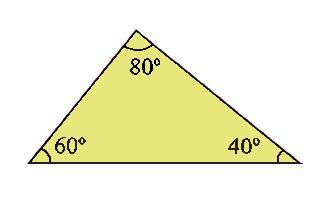
Triângulo acutângulo: são aqueles que apresentam os três ângulos internos com valores inferiores a 90°, sendo, portanto, todos agudos.
Triângulo obtusângulo: chamamos de obtusângulo os triângulos que possuem um dos ângulos com valor maior do que 90°.
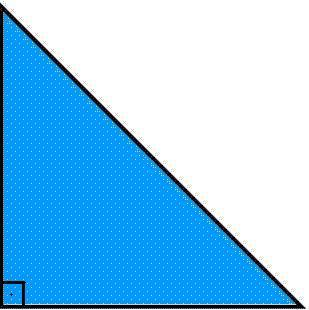
Triângulo retângulo: são aqueles que possuem um dos ângulos reto, ou seja, que mede 90°.
Publicidade
Triângulo escaleno
Como mencionamos anteriormente, o triângulo escaleno é todo e qualquer triângulo que possua medidas diferentes em seus três lados. A classificação dos triângulos escalenos é feita por meio da posição dos lados do triângulo, mas também podemos classifica-los a partir do posicionamento dos ângulos internos. Como possui lados e ângulos diferentes, o triângulo escaleno não apresenta eixos de simetria.
Cálculo da área de um triângulo escaleno
Para calcular a área de um triângulo escaleno, podemos usar o comprimento de um dos lados e a altura, por meio da fórmula A = b.h / 2 onde A é a área, b é a base e h é a altura. Escolha um dos lados do triângulo e use como base, e a altura será relativa à essa base escolhida. Multiplique o valor da base pelo valor da altura, e em seguida divida por 2 para obter o valor da área desse triângulo.
Referências
A matemática do ensino médio – EL Lima, PCP Carvalho, E Wagner, AC Morgado
A arte de resolver problemas – G Polya

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Triângulo escaleno. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/triangulo-escaleno. Acesso em: 22 de December de 2025.
01. [Cesgranrio] Uma rampa plana, de 36 m de comprimento, faz ângulo de 30° com o plano horizontal. Uma pessoa que sobe a rampa inteira eleva-se verticalmente de:
a) 6√3 m.
b) 12 m.
c) 13,6 m.
d) 9√3 m.
e) 18 m.
02. Em um triângulo retângulo, determine as medidas dos ângulos agudos e da hipotenusa, sabendo que um dos catetos mede 3 cm e o outro mede √3 cm.
01. [Podemos representar no triângulo ilustrado a seguir a situação descrita no problema. A hipotenusa representa a rampa percorrida pela pessoa citada:
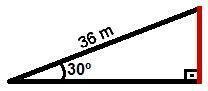
Representação geométrica da questão 1
Na figura, a altura que a pessoa foi elevada está representada pelo lado vermelho (cateto oposto ao ângulo de 30°). Vamos chamar esse lado do triângulo de x para determinar seu valor. Para tanto, utilizaremos a fórmula do seno:
sen 30° = cat. oposto
hipotenusa
1 = x
2 36
2x = 36
x = 36
2
x = 18 m
Portanto, ao subir a rampa, a pessoa eleva-se verticalmente 18 m. Logo, a alternativa correta é a letra e.]
02. [Como sabemos apenas as medidas dos catetos, vamos utilizar o Teorema de Pitágoras para determinar a medida da hipotenusa (h):
(hipotenusa)² = (cateto)² + (cateto)²
h² = 3² + (√3)²
h² = 9 + 3
h = √12
h = 2√3 cm
Considere um ângulo α oposto ao lado de 3 cm. Calculando sua tangente, temos:
tg α = cat. oposto a α
cat. adjacente a α
tg α = 3
√3
tg α = 3
√3
tg α = 3 . √3
√3 √3
tg α = 3√3
3
tg α = √3
Se tg α = √3, logo α = 60°. Sabendo que a soma dos ângulos internos de um triângulo qualquer é 180° e que esse é um triângulo retângulo, podemos determinar a medida de outro ângulo agudo β:
β + α + 90° = 180°
β + 60° + 90° = 180°
β + 150° = 180°
β = 180° – 150°
β = 30°
Portanto, os ângulos agudos desse triângulo valem 30° e 60°.]