Filósofo, Astrônomo e Matemático, Tales de Mileto foi um importante estudioso que trouxe contribuições para suas áreas de atuação. Com seus conhecimentos sobre a Geometria, Tales de Mileto pode observar várias questões em torno dos raios solares. Este, defendia que os raios solares que chegavam ao planeta Terra estavam inclinados e, em cima disso, intitulou a situação de proporcionalidade que relaciona essas retas paralelas e transversais.
A intersecção entre retas paralelas e transversais formando segmentos proporcionais são determinantes do Teorema de Tales, que foi estabelecido por ele.
Publicidade
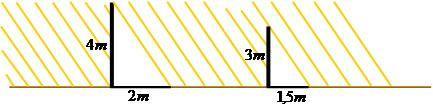
Seguindo o esquema demonstrado na imagem acima, Tales conseguiu medir até mesmo a altura de uma pirâmide, levando em consideração o tamanho de sua sombra. Para isso, fincou uma estaca de madeira na areia e mediu as sombras da pirâmide e da estaca, estabelecendo uma proporção.

Essa mesma proporção pode ser aplicada em outras situações, conforme a imagem abaixo.
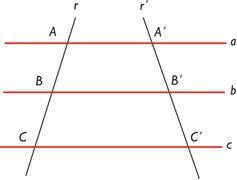
Observando a imagem acima, podemos ver que as retas a, b e c são paralelas, enquanto r e r’ são transversais. Segundo o Teorema de Tales, temos as proporcionalidades demonstradas a seguir:
AB/BC = A’B’/B’C’ ou ainda AB/A’B’ = BC/B’C’
Com essa razão estabelecida, podemos observar que há noções de razão e proporção, ou seja, o segmento de reta AB está para BC, assim como A’B’ está para B’C’. A igualdade que existe entre as duas razões acaba formando uma proporção cujo cálculo poderá ser resolvido por meio de multiplicação cruzada: o produto dos meios é igual ao produto dos extremos. Confira um exemplo abaixo e a aplicação do teorema de Tales para definir o valor do segmento que é desconhecido.
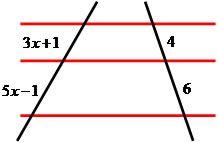
Para a proporção, temos que:
Publicidade
3x+1/5x-1 = 4/6
Resolvendo com multiplicação cruzada, temos que:
20x – 4 = 18x + 6
20x – 18x = 6 + 4
2x = 10
x = 5
Publicidade
Aplicações do Teorema de Tales
O Teorema de Tales apresenta inúmeras aplicações em situações diversas que envolvem distâncias inacessíveis, além de ser muito aplicado na área de Astronomia, em cálculos envolvendo as distâncias. Alguns dos exemplos de aplicação, por exemplo, é analisar plantas de condomínios, instalações elétricas, entre outras diversas situações em áreas diversas do nosso cotidiano.
Referências
www.mat.uc.pt/~pedro/cientificos/Publicacoes/gazeta151PQAP.pdf
https://periodicos.ufsc.br/index.php/revemat/article/viewArticle/12993

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Teorema de Tales. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/teorema-de-tales. Acesso em: 08 de January de 2026.
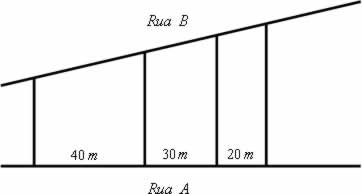
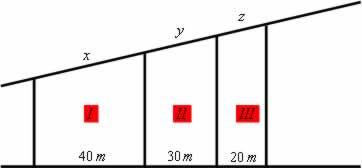
01. [Fuvest–SP] Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de frente para a rua B de cada lote, sabendo que a frente total para essa rua tem 180m?
02. [Saresp–SP] No desenho abaixo estão representados os terrenos I, II e III.
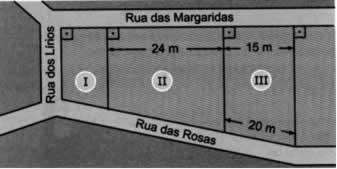
Quantos metros de comprimento deverá ter o muro que o proprietário do terreno II construirá para fechar o lado que faz frente com a Rua das Rosas?
01. 
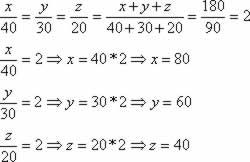
[ Lote I: 80 metros
Lote II: 60 metros
Lote III: 40 metros]
02. 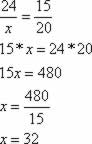
[O muro do terreno II que faz frente com a Rua das Rosas deverá ter 32 metros de comprimento.]