Toda equação do 1° grau que contenha uma ou mais incógnita é considerada uma equação linear. Mas o que acontece se agruparmos 2 ou mais equações lineares? Conheça aqui este agrupamento, conhecido como sistema linear, além de conhecer suas classificações, videoaulas e exercícios resolvidos.
Publicidade
Como classificar um sistema linear?
Antes de mais nada, vamos entender sobre o que estamos falando. É considerado um sistema linear quando existe um conjunto de equações lineares simultâneas com m equações e n incógnitas e é representado da seguinte forma:
Relacionadas
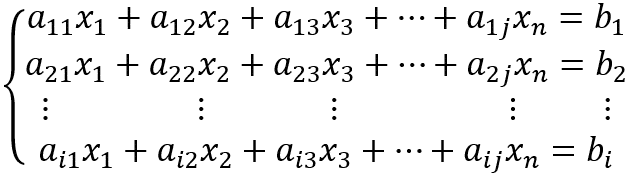
Temos, então, como incógnitas x1, x2, …, xn; já os coeficientes são aij e os termos independentes são os bi.
Entretanto, alguns sistemas possuem soluções, outros não e alguns admitem várias soluções. Desta forma, vamos entender cada um deles.
Sistema possível e determinado (S.P.D.)
Esse tipo de sistema linear admite apenas uma única solução. Vamos ver um exemplo disso:
Publicidade
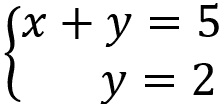
Neste caso, a única solução permitida para o sistema é o par (3,2), ou seja, a solução seria x = 3 e y = 2.
Sistema possível e determinado (S.P.I)
O S.P.I é um sistema linear que admite mais de uma solução. Como exemplo, temos o sistema a seguir:
Publicidade
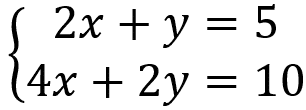
Para este exemplo, a solução deste sistema linear são vários como os pares (2,1); (0,5); (4,-3) etc.
Sistema impossível (S.I)
Este sistema não possui solução alguma. Tomemos como exemplo o sistema abaixo:
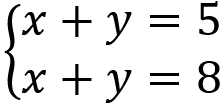
Este sistema não possui solução, pois não existem dois números x e y, em que a soma seja 5 e, ao mesmo tempo, a soma também seja 8.
Estes são os 3 tipos de sistemas lineares que podemos encontrar em livros didáticos e exercícios. Para que você tenha uma melhora compreensão do assunto estudado até aqui, apresentaremos a seguir alumas videoaulas!
Saiba mais sobre sistemas lineares
Para que seus estudos possam render mais ainda, apresentamos a seguir algumas videoaulas sobre o que foi estudado até aqui!
Conceitos iniciais sobre sistemas lineares
Ter os conceitos básicos sobre qualquer assunto é de extrema importância. Este vídeo apresenta alguns conceitos sobre sistemas lineares para que você possa se dar muito bem na hora dos exercícios!
Resolvendo um sistema linear por escalonamento
Para se resolver um sistema linear, é necessária alguma prática e conhecimento dos métodos para resolvê-los. Pensando nisso, apresentamos aqui neste vídeo o método do escalonamento para que seus exercícios não fiquem tão difíceis!
Resolvendo um sistema linear pelo método de Cramer
Outro método para que você possa se dar bem nos exercícios é o método de Cramer. Este vídeo irá te auxiliar nos estudos sobre o método.
Por fim, é recomendado que você faça uma breve revisão sobre equações de primeiro grau, assunto encontrado aqui mesmo no site!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Sistema linear. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/sistema-linear. Acesso em: 19 de April de 2025.
1. [Fuvest-SP]
Carlos e sua irmã Andreia foram com seu cachorro Bidu à farmácia de seu avô. Lá encontraram uma velha balança com defeito, que só indicava corretamente pesos superiores a 60 kg. Assim, eles se pesaram dois a dois e obtiveram as seguintes marcas:
Carlos e o cão pesam juntos 87 kg;
Carlos e Andreia pesam 123 kg;
Andreia e Bidu pesam 66 kg.
Determine o peso de cada uma deles:
Vamos considerar a seguinte situação:
Andreia: a
Bidu: b
Carlos: c
Vamos montar o seguinte sistema linear:
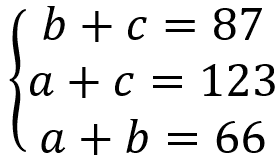
Pelo método de Cramer, vamos montar o determinante com as incógnitas e resolve-lo. Assim
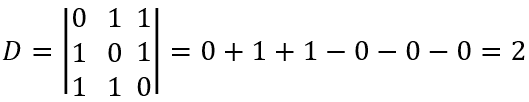
Vamos determinar Db. Assim
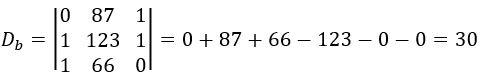
Sabemos que b = Db/D. Dessa forma
b = 30/2
b = 15
Usando o sistema linear para resolver as outas incógnitas, temos que
b + c = 87
15 + c = 87
c = 87 – 15
c = 72
a + b = 66
a + 15 = 66
a = 66 – 15
a = 51
Portante Andreia pesa 51Kg, Bidu 15 kg e Carlos 72 kg.
2. [Vunesp – SP]
Um clube promoveu um show de música popular brasileira ao qual compareceram 200 pessoas, entre sócios e não sócios. No total, o valor arrecadado foi de R$ 1 400,00 e todas as pessoas pagaram ingresso. Sabendo que o preço do ingresso foi R$ 10,00 e que cada sócio pagou metade desse valor, determine o número de sócios e não sócios que compareceram ao show.
Vamos considerar a seguinte situação:
x: sócios
y: não sócios
Vamos então montar o sistema para esse problema:
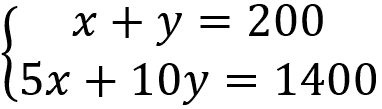
Iremos resolver esse sistema pelo método da substituição. Dessa forma vamos isolar x na 1° equação:
x = 200 – y
Agora, vamos substituir x na 2° equação e resolver para y:
5(200 – y) + 10y = 1400
1000 – 5y +10y = 1400
5y + 1000 = 1400
5y = 1400 – 1000
5y = 400
y = 400/5
y = 80
Dessa forma, vamos substituir y na 1° equação e resolver para x:
x + 80 = 200
x = 200 – 80
x = 120
Portanto, no show estavam presentes 120 sócios e 80 não sócios.