Secante

A secante é a uma razão trigonométrica. Assim como a cossecante e a cotangente. Elas são inversas das razões cosseno, seno e tangente, respectivamente. Estudar o que é cada uma dessas razões é importante para o aprofundamento nos estudos da trigonometria. Veja o que é, sua fórmula e seu gráfico.

Publicidade

O que é a secante

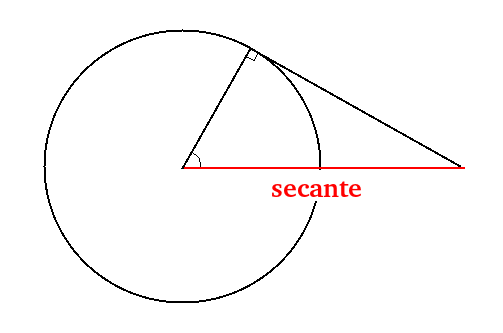
A secante é a razão trigonométrica inversa do cosseno. Assim, por definição, essa razão trigonométrica pode ser como a recíproca do cosseno. Além disso, em um triângulo retângulo, ela é definida como a razão entre a hipotenusa pelo cateto adjacente. Ela é usada para calcular relações nas quais são necessários estudar os ângulos internos de um triângulo retângulo.

Fórmula

Matematicamente, a secante é o inverso do cosseno. Além disso, como o cosseno é a razão entre o cateto adjacente e a hipotenusa de um triângulo retângulo, a razão inversa é a razão entre o cateto adjacente e a hipotenusa. Ou seja:

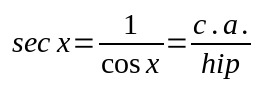
Em que,

• sec x: secante do ângulo x
• cos x: cosseno do ângulo x
• c.a.: cateto adjacente
• hip: hipotenusa

Por ser uma razão, essa função trigonométrica não possui unidade de medida. Além disso, assim como as outras identidades trigonométricas, ela também é periódica.

Publicidade

Gráfico

Assim como as demais razões trigonométricas, é possível fazer o gráfico da sequência. Nesse caso, haverá pontos nos quais o gráfico não está definido. Isso acontece porque os pontos não estão no domínio da função.

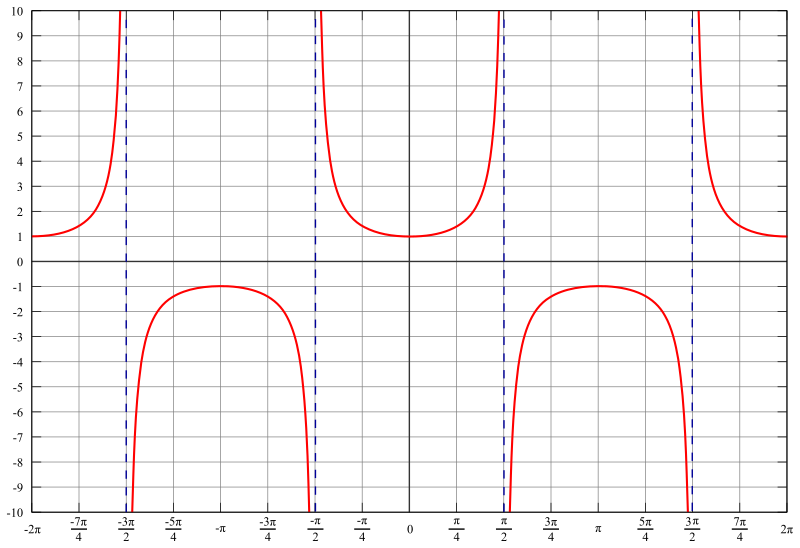
Os pontos nos quais o gráfico dessa razão trigonométrica não está definido são aqueles nos quais o cosseno do ângulo é igual a zero. Ou seja, em valores iguais a (2n-1)π/2, desde que n seja um número natural, diferente de zero. Por exemplo, π/2, 3π/2, 5π/2 etc.

Vídeos sobre secante

O estudo das funções trigonométricas pode parecer amedrontador. Porém, com paciência fica fácil compreendê-las. Além disso, elas podem ser aplicadas em diversas outras áreas do conhecimento. Por exemplo, na Física. Dessa maneira, veja os vídeos selecionados:

Publicidade

Relações trigonométricas no triângulo retângulo

O triângulo retângulo é um elemento muito importante para a Matemática. Por isso, a Professora ngela, de Matemática, ensina como encontrar as principais relações trigonométricas em um triângulo retângulo. Ao longo do vídeo, a professora relaciona as medidas dos lados com os ângulos internos e chega às identidades trigonométricas desejadas.

Secante, cossecante e cotangente

Além das identidades trigonométricas, existem as razões trigonométricas. Elas são a secante, cotangente e cossecante. Nesse vídeo do canal Equaciona com Paulo Pereira é possível compreender cada uma dessas razões. Além disso, o professor Paulo dá exemplos de cada uma dessas razões.

Funções secante e cossecante

O professor Gustavo Adolfo explica como é possível calcular algumas funções trigonométricas. Em específico, o docente fala sobre as funções inversas do seno e do cosseno. Além disso, o professor também ensina de que maneira é possível desenhar o gráfico de cada uma dessas funções.

As relações e razões trigonométricas são muito usadas em diversos casos. Por exemplo, no estudo da Mecânica. Além disso, essas relações são fundamentais para o estudo da trigonometria. Dessa maneira, estude mais e aprofunde seus conhecimentos sobre o triângulo retângulo.

Referências