Em algumas situações, é necessário multiplicar o mesmo número várias e várias vezes. Essa tarefa pode acabar se tornando um pouco extensa demais e até mesmo confusa. Para facilitar essa processo, utiliza-se a potenciação.
Publicidade
Aqui, vamos estudar os conceitos de potenciação, suas propriedades, as operações matemáticas e a relação entre potenciação e radiciação.
O que é potenciação
Suponha que você possui um total de R$100,00 em dinheiro. Você, por algum motivo, deseja saber qual seria o valor desse dinheiro se ele fosse multiplicado por ele mesmo 10 vezes seguidas.
Certamente isso levaria algum tempo. Para facilitar a conta, podemos utilizar a potenciação.
![]()
De acordo com a imagem acima, podemos identificar os seguintes elementos:
- a: base da potenciação (número que está sendo multiplicado por ele mesmo);
- n: expoente (número de vezes que a base está sendo multiplicada).
Segundo o nosso exemplo, a base a seria os R$100,00 e o o expoente n seria as 10 vezes desejadas.
Publicidade
Como ler potenciação
Existem diversas maneiras de se ler uma potenciação. Isto se deve ao expoente, pois é ele quem determina a forma de falar da potenciação.
Se a base for 3, e alterarmos apenas o expoente, começando de n = 2, teremos as seguintes nomenclaturas:
- 32: três ao quadrado ou três elevado à segunda potência;
- 33: três ao cubo ou três elevado à terceira potência
- 34: três elevado à quarta potência
- 35: três elevado à quinta potência
- 36: três elevado à sexta potência
- 37: três elevado à sétima potência
- 38: três elevado à oitava potência
- 39: três elevado à nona potência
Conforme o expoente for aumentando, a nomenclatura segue o padrão.
Publicidade
Propriedades da potenciação
Assim como em muitos assuntos da matemática, a potenciação também possui algumas propriedades básicas. Dessa maneira, vamos compreender algumas dessas propriedades.
Potenciação de número negativo
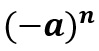
Para base de números negativos existem duas propriedades. Assim, podemos defini-las da seguinte forma:
- Se o expoente for par, então o resultado será positivo;
- Porém, se o expoente for ímpar, então o resultado será negativo.
Em resumo, suponha que a base seja -3. Se tivermos um expoente n = 2, então o resultado será 9. Mas se n = 3, então o resultado será -27.
Potenciação de fração
Sendo a base uma fração, teremos a seguinte situação:
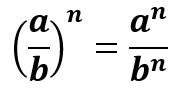
Desse modo, obtemos como resultado o numerador e o denominador da fração ambos elevados ao expoente n.
Operações matemáticas com potenciação
Algumas operações envolvendo a potenciação são necessárias para o desenvolvimento de alguns exercícios, pois essas operações facilitam os cálculos.
Produto de potências de mesma base
![]()
Quando se realiza uma multiplicação de duas bases iguais, segundo a imagem acima, repetimos a base e somamos os expoentes.
Potência de expoente inteiro negativo
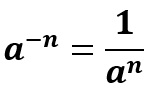
Para um expoente negativo, obtemos como resultado o inverso do valor da base elevada ao mesmo expoente. Supondo a base como sendo 2 e o expoente n = -2, o resultado obtido seria 1/22.
Divisão de potências de mesma base
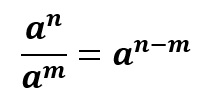
Ao contrário do produto de bases iguais, em que se somam os expoentes, na divisão de bases iguais os expoentes se subtraem, conforme podemos observar na imagem acima.
Potência de potência
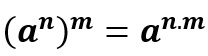
Neste caso, devemos apenas multiplicar os expoentes.
Potência de um produto
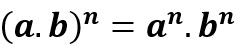
Nessa operação, obtemos como resultado o produto dos números a e b, cada um elevado ao expoente n.
Podemos aplicar essas operações a diversos problemas, facilitando assim suas resoluções.
Potenciação e radiciação
A radiciação utiliza as mesmas características que a potenciação. Assim, podemos utilizar as mesmas propriedades que a potenciação.
Entenda mais sobre potenciação
Por fim, podemos aprender um pouco mais sobre esse assunto assistindo aos próximos vídeos.
Definição de potenciação
Nesse vídeo, é possível absorver um pouco mais sobre as definições e propriedades da potenciação.
Operações com potenciação
Esse vídeo mostra, similarmente o que foi explicado um pouco mais acima, a respeito das operações com potenciação.
Regras de potenciação
Por último, vamos entender um pouco mais sobre as regras de potenciação.
Uma função exponencial só é compreendida se os estudos de potenciação estiverem muito bons. Por isso, estudaremos sobre esse assunto em outra oportunidade.
Referências
Luiz Roberto Dante, Matemática: contexto & aplicações;
Manoel Paiva, Matemática.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Potenciação. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/potenciacao. Acesso em: 31 de March de 2025.
1. [FUVEST -SP 2012]
O valor de (0,2)3 + (0,16)2 é:
a) 0,0264
b)0,0336
c)0,1056
d)0,2568
e)0,6256
Como (0,16)2 = (0,4)4, temos que
(0,2)3 + (0,4)4 = 0,008 + 0,0256 =0,0336
A resposta correta é a letra b.
2. [FATEC]
Das três sentenças abaixo:
I. 2x+3 = 2x . 23
II. (25)x = 52x
III. 2x + 3x = 5x
a) somente a I é verdadeira;
b) somente a II é verdadeira;
c) somente a III é verdadeira;
d) somente a II é falsa;
e) somente a III é falsa.
Para a primeira expressão, vale a propriedade de produtos de mesma base.
Para a segunda expressão, a potência de potência pode ser utilizada, pois
(25)x = (52)x = (5)2x
Porém, para a última expressão, não existe nenhuma operação que se possa realizar com ela.
Portanto, a resposta correta é a letra e.