O que aconteceria se agruparmos várias formas geométricas, por exemplo os triângulos, em uma única forma geométrica 3D fechada? Isso é conhecido como poliedros. Entenda aqui o que eles são e a sua classificação. No fim, será apresentado algumas videoaulas sobre este assunto para que você possa compreendê-lo melhor.
Publicidade
O que são os poliedros?
Você já deve ter observado como é formada a superfície de uma bola de futebol. Caso não tenha, ela é formada por várias peças poligonais costuradas lado a lado. O formato arredondado da bola se deve à pressão interna do ar. Caso isso não ocorresse, a superfície se assemelharia ao seguinte formato:
Relacionadas

Em outras palavras, os poliedros são formas geométricas constituídos polígonos planos, além de possuírem vértices, arestas e faces. Desta forma, iremos estudar a classificação dos poliedros que são duas: poliedros convexos e não convexos.
Classificação dos poliedros
Podemos dividir os poliedros em duas classes: em convexos e não convexos. Vamos então estudar cada um deles separadamente.
Poliedro convexo: um poliedro é convexo se um segmento de reta estiver contido inteiramente no poliedro. Observe a figura a seguir como exemplo.
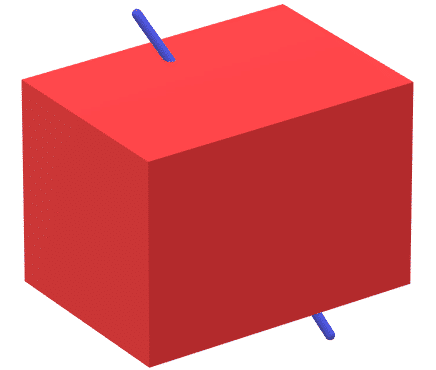
Poliedro não convexo: se uma reta, ao passar por um poliedro, tocar em 3 ou mais faces deste poliedro, então, ele é não convexo. A seguir, temos um exemplo disso.
Publicidade
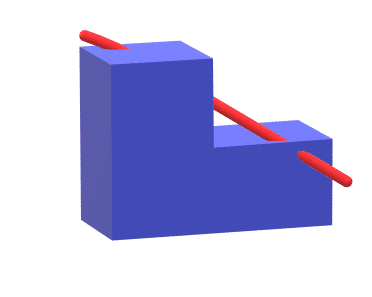
Além destas duas formas, podemos também encontrar poliedros convexos regulares. Este tipo de poliedro será classificado como convexo regular se – e somente neste caso – são satisfeitas as seguintes condições:
- todas as suas faces são regiões poligonais regulares e congruentes entre si;
- todos os seus ângulos poliédricos são congruentes entre si.
Existem exatamente cinco classes de poliedros regulares. São eles: tetraedro regular, hexaedro regular, octaedro regular, dodecaedro regular e icosaedro regular. A imagem a seguir representa um exemplo de cada uma dessas classes.
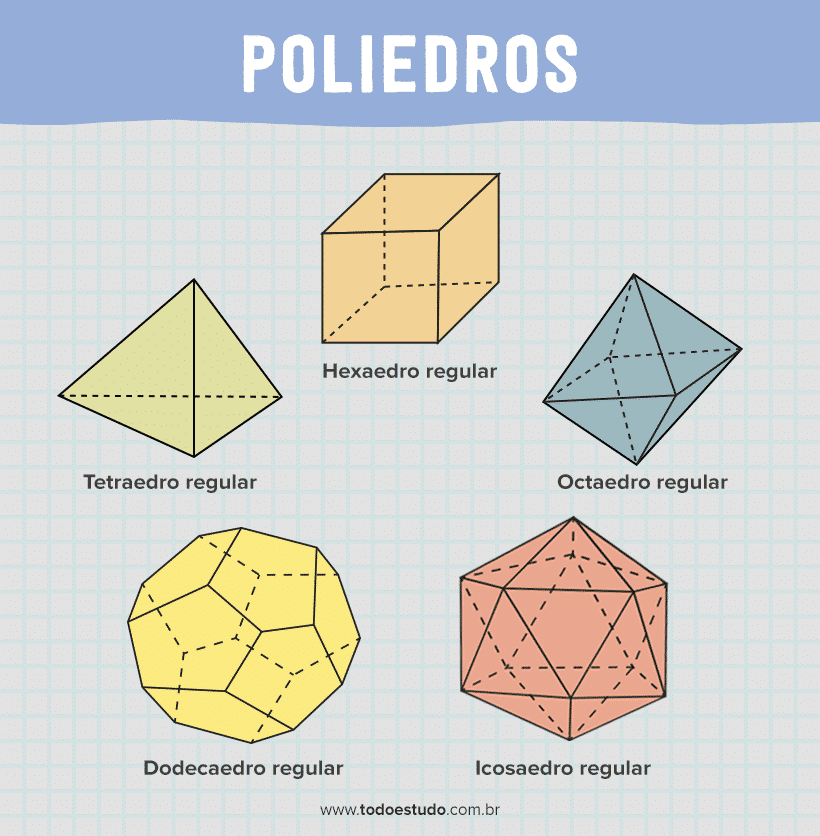
Estas figuras foram as formas de poliedros existentes. Para que você possa ter um melhor entendimento sobre o assunto, apresentamos a seguir algumas videoaulas!
Publicidade
Saiba mais sobre poliedros
Para que os seus estudos possam render muito mais, a seguir segue uma pequena lista com algumas videoaulas!
Conceitos sobre poliedros
Neste vídeo, é apresentado alguns conceitos básicos sobre poliedros, além de apresentar também a relação de Euler.
Poliedros de Platão
Caso você tenha dúvidas ou não sabe sobre o que se trata, este vídeo apresenta os poliedros de Platão para que você possa compreender de vez sobre este assunto!
Exercícios
Sempre é bom entender a teoria na prática! Pensando nisso, este vídeo apresenta alguns exercícios resolvidos sobre poliedros para que você possa se dar muito bem nas provas!
Por fim, sempre é bom revisar alguma matéria que da base para o conceito de poliedros. A recomendação é estudar sobre geometria espacial e polígonos. Assim, seus estudos serão completos!
Referências
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Poliedros. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/poliedros. Acesso em: 02 de April de 2025.
1.
Sabendo que um poliedro possui 20 vértices e que em cada vértice se encontram 5 arestas, determine o número de faces dessa figura.
O número de vértices é 20, logo V = 20.
Como as arestas que saem e chegam até o vértice são as mesmas, então devemos dividir por dois o número total de arestas. Dessa forma:
A = (5*20)/2 = 50
Podemos então utilizar a relação de Euler. Logo
F + V = A + 2
F + 20 = 50 + 2
F = 52 – 20
F = 32
Portanto, o poliedro possui 32 faces.
2. [FAAP-SP]
Num poliedro convexo, o número de arestas excede o número de vértices em 6 unidades. Calcule o número de faces.
Segundo o enunciado, temos que o número de aresta possui 6 unidades a mais que o número de vértices. Logo, temos que
A = V + 6
Sabemos que a relação de Euler é dada por
F + V = A + 2
Vamos então substituir A = V + 6 na relação de Euler. Assim
F + v = V + 6 + 2
F = 8
Portanto, o poliedro possui 8 faces.