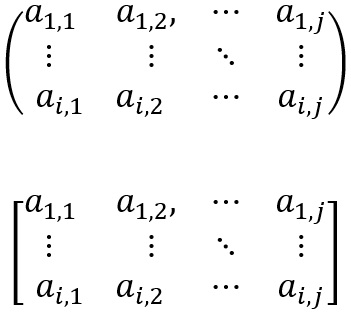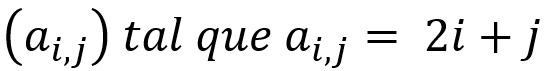Em jornais ou revistas, é comum encontrar informações em forma de tabelas. Além disso, muitas empresas utilizam bancos de dados, que são coleções de tabelas que se relacionam entre si. Para esse tipo de organização, dá-se o nome de matrizes. Confira abaixo mais detalhes sobre representação, tipos, operações, equações matriciais e determinante de uma matriz, além de exercícios resolvidos.
Publicidade
O que são matrizes
Uma matriz nada mais é do que dados organizados em uma tabela. Isso facilita a organização e a interpretação dos dados. De uma maneira mais geral, é possível definir uma matriz da seguinte forma:
Relacionadas
Denomina-se matriz m x n (lê-se m por n) uma tabela retangular formada por m x n números reais, dispostos em m linhas e n colunas.
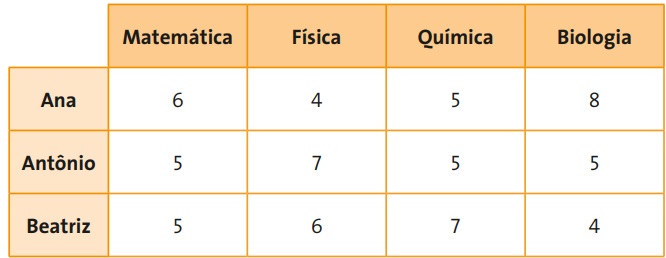
A imagem acima pode ser representada por uma matriz A 4X3 (4 linhas e 3 colunas). Cada número que está na tabela acima pode ser chamado de elemento de uma matriz. Por exemplo, o número 6 está na linha 1 e coluna 1, porém o elemento 4 está na linha 3 e coluna 4. De uma forma geral, podemos representar um elemento de uma matriz como sendo ai,j, em que i é o numero da linha e j o número da coluna.
Representação
Existem duas formas de se representar uma matriz: explicitamente e implicitamente. Essas duas representações podem ser usadas separadamente ou em conjunto, dependendo do contexto. Assim, as representações seriam:
Publicidade
- Explicitamente: é uma forma representada por parênteses ou colchetes;

- Implicitamente: uma forma mais genérica, ou seja, como uma “lei” que determina os elementos ai,j da matriz. Um exemplo seria:

O entendimento das representações matriciais são importantes, pois podemos construir matrizes apenas pela forma implícita ou realizar operações matriciais diretas a partir da forma explícita.
Tipos de matrizes
Muitas são as possibilidades de existir um determinado tipo de matriz, pois o tamanho dela depende da quantidade de linhas e da quantidade de colunas. Dessa forma, conheça abaixo alguns desses tipos especiais de matriz:
Matriz linha

Publicidade
Como o próprio nome já diz, a matriz linha possui apenas uma linha – com a possibilidade de ter várias colunas, como indica a figura acima.
Matriz coluna
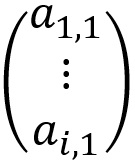
Diferente da matriz linha, a matriz coluna possui uma única coluna e várias linhas.
Matriz quadrada

Para que uma matriz possa ser chamada de quadrada, a quantidade de linhas e colunas deve ser igual, ou seja, m = n. No exemplo da figura acima, tem-se uma matriz quadrada de ordem 3 (3×3).
Matriz diagonal
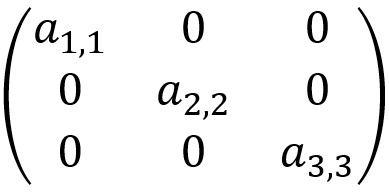
A matriz diagonal é uma matriz quadrada de ordem n que possui os elementos da diagonal principal diferentes de zero, sendo que os demais são iguais a zero.
Matriz nula
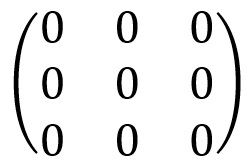
No conjunto das matrizes, uma matriz que possui todos os seus elementos iguais a zero é chamada de matriz nula. A ordem dela não interfere no nome, ou seja, ela pode ser uma matriz quadrada ou não.
Matriz identidade

Quando os elementos da diagonal principal de uma matriz quadrada de ordem n forem todos iguais a 1, então a matriz é chamada de matriz identidade.
Matriz oposta
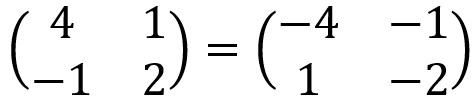
Seja a matriz A = (ai,j)m x n. Chama-se oposta de A a matriz representada por -A , tal que A + (-A) = 0m x n, sendo 0m x n a matriz nula do tipo m x n.
Matriz transposta
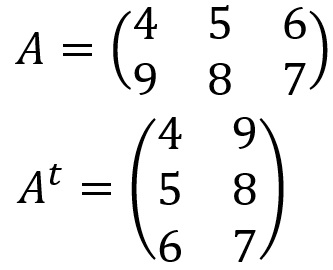
Seja A uma matriz de ordem m x n. A sua transposta é dada por At = (a’j,i)n x m. Na prática, a transposta de A é obtida trocando, de uma forma ordenada, suas linhas pelas colunas.
Matriz inversa
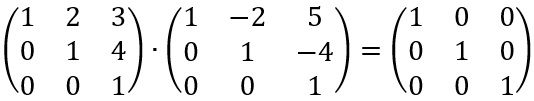
Sejam A e B duas matrizes, ambas quadradas de ordem n. Se fizermos a multiplicação de A por B e o resultado for uma matriz identidade, então B é chamada de inversa da matriz A.
Com isso em mente, é possível entender agora sobre as operações entre matrizes, pois o conhecimento dos tipos apresentados anteriormente são necessários para o próximo tópico.
Operações entre matrizes
Quando se fala em um determinado conjunto de números, mesmo quando são agrupados em tabelas como as matrizes, é possível realizar algumas operações matemáticas com eles. Porém, para matrizes, existem certas diferenças nas operações a serem realizadas. Entenda um pouco mais sobre isso:
Igualdade de matrizes
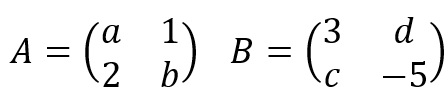
Duas matrizes A e B são iguais se forem de mesma ordem, ou seja, m x n, e todos os elementos correspondentes forem iguais. Ou seja, se A = (ai,j)m x n e B = (bi,j)m x n, tem-se que A = B se ai,j = bi,j, para todo i e para todo j.
Usando a imagem acima, tomemos as duas matrizes A e B. Elas serão iguais se tivermos a seguinte relação:
- a = 3
- 1 = d
- 2 = c
- b = -5
Adição de matrizes
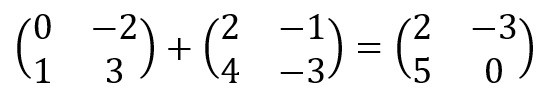
Considere as duas matrizes A e B acima, respectivamente. A soma de A com B (representada por A + B) é a matriz C = (ci,j)m x n, em que ci,j = ai,j + bi,j. Em outras palavras, a matriz soma C tem a mesma ordem de A e B e seus elementos são a soma dos elementos correspondentes de A e B.
Subtração de matrizes
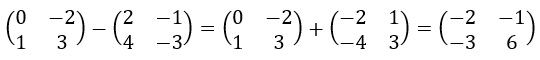
Na subtração, utiliza-se os o conceito de matriz oposta. Assim, seja A a matriz à esquerda da subtração acima e B a matriz da direita. A diferença entre A e B, representa por A – B, é a soma de A com a oposta de B, como é visto na figura acima.
Multiplicação de um número real por uma matriz
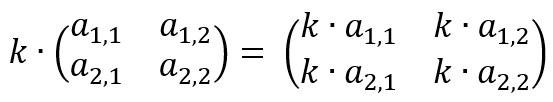
Ao se multiplicar uma matriz A por um número real qualquer k, obtemos uma outra matriz B de tal forma que o resultado é B = k ∙ A. Isso significa que B é obtida multiplicando todos os elementos de A pelo número real k.
Multiplicação de matrizes
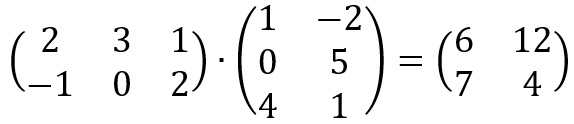
Essa operação não é tão simples como as outras até aqui estudadas, pois não basta apenas multiplicar os elementos correspondentes um por um. Vamos introduzir a definição matemática da multiplicação e depois vamos entendê-la passo a passo.
Dadas as matrizes A = (aij)m x n e B = (bij)n x p, chama-se produto de A por B, e se indica por AB, a matriz C = (cik)m x p, em que cik = ai1 ∙ b1k + ai2 ∙ b2k + ai3 ∙ b3k + ai4 ∙ b4k + … + ain ∙ bnk; para todo iϵ{1, 2, …, m} e todo kϵ{1, 2, …, p}.
Com a definição em mente, vamos então entendê-la. Antes de mais nada, é importante perceber que a multiplicação AB só existe quando o número de colunas de A for igual ao número de linhas de B. Além disso, a matriz resultante dessa multiplicação possui o número de linhas de A e o número de colunas de B.
Acompanhe abaixo o procedimento para resolver a multiplicação das duas matrizes representadas na figura que está no começo deste tópico:
1°) Vamos multiplicar a primeira linha de A pela primeira coluna de B, ordenadamente, e somar cada multiplicação. O resultado será: c1,1 = 2∙1 + 0∙3 + 1∙4 = 6;
2°) Para o elemento c2,1, pegamos a primeira linha de A e a segunda linha de B e realizamos o mesmo processo do passo anterior. Logo: c1,2 = 2∙(-2) + 3∙5 + 1∙1 = 12;
3°) Utilizando o mesmo processo para a segunda linha de A com a primeira coluna de B, obtemos que: c2,1 = (-1)∙(1) + 0∙0 + 2∙4 = 7;
4°) Por último, temos que a multiplicação da segunda linha de A com a segunda coluna de B conseguimos obter que: c2,2 = (-1)∙(-2) + 0∙5 + 2∙1 = 4.
As operações matriciais são de fundamental importância para a resolução de muitos exercícios. Além disso, são de extrema necessidade em algumas aplicações do dia a dia, como a formação de imagens em computadores.
O que são equações matriciais
De um modo geral, quando pensamos em equações, vem à mente “encontrar o valor da incógnita x“. Mas e quando nos deparamos com uma equação que envolve matrizes? A ideia é a mesma, porém o que é preciso encontrar é uma matriz incógnita, e não mais apenas um valor numérico único.
Vejamos um exemplo: dado duas matrizes A e B, encontre a matriz X de tal forma que X – A = B. As matrizes A e B são definidas a seguir como:
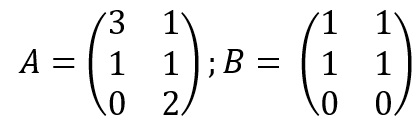
Essa equação pode ser resolvida isolando a matriz incógnita, ou seja, X = A + B. Em seguida, substituímos as matrizes A e B e resolvemos então a equação matricial.
Determinantes
De certa forma, existe um número real associado a uma matriz quadrada. A esse número, dá-se o nome de determinante. A seguir, vamos estudar os determinantes de ordem 2, 3 e os de ordem maiores que 3.
Determinantes de matrizes de ordem 2 e 3
Um determinante de ordem 2 é obtido realizando a multiplicação cruzada entre os elementos de uma matriz A e, em seguida, subtraindo essa multiplicação, como mostrado na figura abaixo:
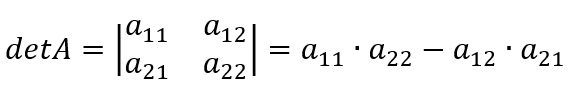
Por outro lado, o determinante de ordem 3 é obtido de uma maneira um pouco diferente. Utilizamos aqui a regra de Sarrus, mostrada a partir da figura a seguir:
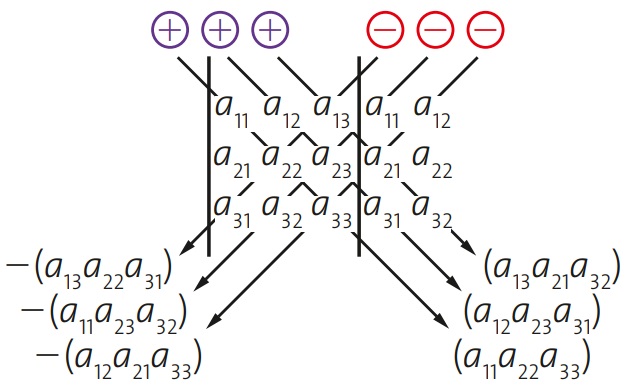
O resultado final dessa regra é o determinante a seguir:
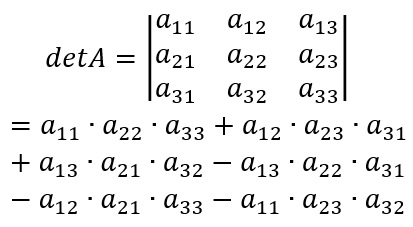
Por fim, as matrizes são muito importantes para o dia a dia. Um exemplo disso é a utilização de matrizes em computação gráfica. Além disso, é possível utilizar as matrizes e os determinantes em sistemas lineares de equações. Aproveite para estudar sobre esse conteúdo também!
Referências
Matemática: ciência e aplicações: ensino médio – Gelson Iezzi [et. al.]
Matemática: contexto & aplicações: ensino médio – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Matrizes. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/matrizes. Acesso em: 11 de July de 2025.
1. [PUC–SP–Adaptada]
São dadas as matrizes A = (aij) e B = (bij), quadradas de ordem 2, com aij = 3i + 4j e bij = – 4i – 3j. Considerando C = A + B, calcule a matriz C.
Pela regra geral de A = aij = 3i + 4j, temos que
a11 = 3∙1 + 4∙1 = 7
a12 = 3∙1 + 4∙2 = 11
a21 = 3∙2 + 4∙1 = 10
a22 = 3∙2 + 4∙2 = 14
Para B, temos que bij = – 4i – 3j, assim
b11 = – 4∙1 – 3∙1 = -7
b12 = – 4∙1 – 3∙2 = -10
b21 = – 4∙2 – 3∙1 = -11
b22 = – 4∙2 – 3∙2 = -14
Assim, as matrizes A e B são
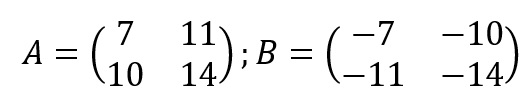
Logo, a soma C = A + B será
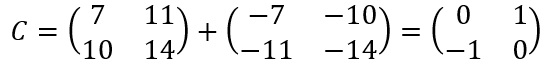
2. [(UFG)]
Um modelo matemático usado para ampliação de uma imagem consiste em considerar uma transformação linear dada pela multiplicação de uma matriz escala Es por uma matriz coluna A, composta pelas coordenadas do ponto P, que forma a imagem que será ampliada. Considerando as matrizes A e Es dadas por
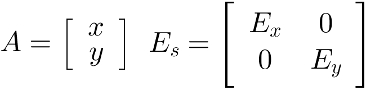
em que Ex e Ey são fatores multiplicativos que indicam a mudança da escala, então a matriz Q que indica as novas coordenadas do ponto P, obtidas pela multiplicação das matrizes Es e A, é:
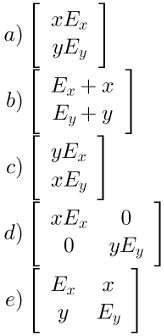
É muito provável que o estudante se esqueça de que a multiplicação de matrizes não é comutativa, isto é, multiplicar A por Es não obrigatoriamente resulta no mesmo resultado que multiplicar Es por A. Confira a multiplicação de Es por A, que é a solicitada no texto do exercício:
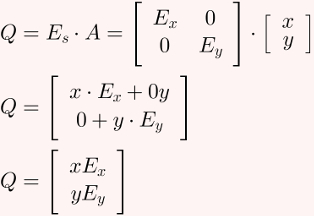
RESPOSTA: a)