Fundamental no estudo da trigonometria, principalmente no que se refere aos triângulos A lei dos cossenos é um método usado para calcular algumas das questões envolvendo triângulos quaisquer, que não sejam retângulos. Os triângulos em questão, por não apresentarem ângulos retos, não têm relações trigonométricas do seno, cosseno e tangente válidas.
Publicidade
Para conseguirmos, portanto, encontrar as medidas de ângulos e lados desses triângulos mencionados, devemos usar a lei dos cossenos, expressa pela lei:
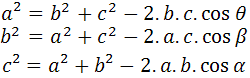
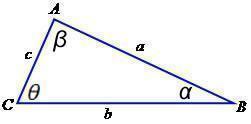
Para quem tem dificuldade para decorar fórmulas, alguns professores desenvolveram dicas. Podemos obsercar que o ângulo usado para o cosseno será sempre o ângulo oposto ao que inicia a fórmula. Para que seja feito o cálculo, portanto, da medida de um lado do triângulo qualquer, precisamos que seja informado pelo menos a medida dos dois lados e o valor do cosseno do ângulo oposto ao lado que queremos calcular.
A lei dos cossenos estabelece que o quadrado de um dos lados é igual à soma dos quadrados dos outros dois lados, menos o dobro do produto dos dois lados pelo cosseno do ângulo entre eles, que está exposto na fórmula acima. A lei dos cossenos pode calcular qualquer coisa a partir do Teorema de Pitágoras, que estabelece que “A soma dos quadrados de seus catetos corresponde ao quadrado de sua hipotenusa”.
Publicidade
Referências
Conecte Matemática – Gelson Iezzi, Osvaldo Dolce

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Lei dos Cossenos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/lei-dos-cossenos. Acesso em: 08 de July de 2025.
01. Calcule a medida da maior diagonal do paralelogramo da figura a seguir, utilizando a lei dos cossenos.
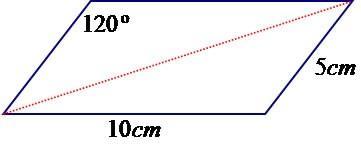
cos 120º = –cos(180º – 120º) = – cos 60º = – 0,5
02. Em um triângulo ABC, temos as seguintes medidas: AB = 6 cm, AC = 5 cm e BC = 7 cm. Determine a medida do ângulo A.
Vamos construir o triângulo com as medidas fornecidas no exercício.
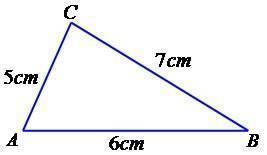
Aplicando a lei dos cossenos
a = 7, b = 6 e c = 5
01. [x² = 5² + 10² – 2 * 5 * 10 * ( – cos 60º)
x² = 25 + 100 – 100 * (–0,5)
x² = 125 + 50
x² = 175
√x² = √175
x = √5² * 7
x = 5√7]
02. [7² = 6² + 5² – 2 * 6 * 5 * cos A
49 = 36 + 25 – 60 * cos A
49 – 36 – 25 = –60 * cos A
–12 = –60 * cos A
12 = 60 * cos A
12/60 = cos A
cos A = 0,2]