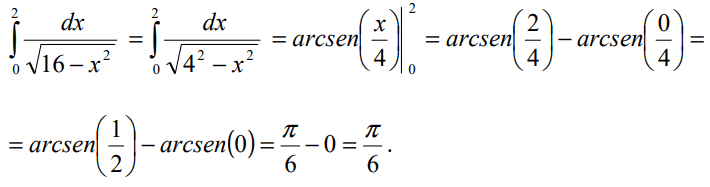Sabemos calcular áreas de regiões simétricas, mas como calcular áreas de regiões curvas não simétricas? Entenda como isso é possível a partir da ideia de integrais, além da diferença entre integral definida e indefinida. No fim, veja vídeos sobre o assunto para fixar e aprofundar os conceitos estudados!
Publicidade
O que são integrais e para que servem?
O conceito da integral surgiu a partir da necessidade de se calcular a área de uma região curva não simétrica. Por exemplo, a área sobre o gráfico da função f(x) = x² é difícil de ser calculada, pois não existe uma ferramenta exata para isso.
Relacionadas
Outro problema conhecido é o da distância. Sabemos calcular a distância percorrida por um objeto quando sua velocidade é constante. Isso também pode ser feito através do gráfico de velocidade em função do tempo. Mas, quando essa velocidade não é constante, não conseguimos calcular a distância de uma maneira tão simples.
Essas foram algumas das situações para o surgimento da integral, mas a integral possui várias aplicações além dessas, como o cálculo de áreas, volumes e suas aplicações na física e na biologia. Vale ressaltar também que isso é apenas um resumo do que seria uma integral, pois sua definição é puramente matemática e requer algum conhecimento em cálculo de limites.
Integral definida x indefinida
Vamos, então, estudar sobre duas formas de integrais: integral definida e integral indefinida. Abaixo, você vai entender a diferença e ver como se calcula cada uma delas.
Integral definida
Suponhamos uma função f(x) cujo gráfico seja curvo e que seja definida em um intervalo de a até b. Vamos então desenhar alguns retângulos dentro desse intervalo da função f(x), conforme a imagem a seguir.
Publicidade
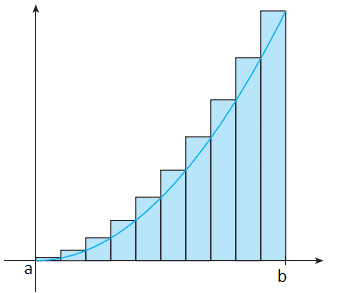
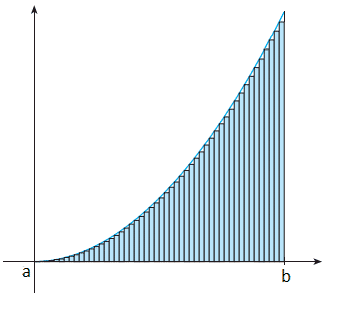
Considerando que temos n retângulos na imagem anterior, ao tendermos o valor de n para infinito, saberemos com exatidão o valor da área dessa função.
Publicidade
Essa é uma definição informal de uma integral definida. Uma definição formal é apresentada a seguir.
Se f é uma função contínua definida em a≤x≤b, dividimos o intervalo [a, b] em n subintervalos de comprimentos iguais Δx=(b-a)/n. Sejam x0(=a), x1,x2, . . . , xn(=b) as extremidades desses subintervalos, escolhemos os pontos amostrais x*1 , x*2 , …, x*n nesses subintervalos, de forma que x*i esteja no i-ésimo subintervalo [xi-1, xi]. Então, a integral definida de f de a a b é
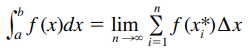
desde que este limite exista. Se ele existir, dizemos que f é integrável em [a, b].
A integral definida pode ser interpretada como a área resultante de uma região. Além disso, ela é um valor em seu resultado, ou seja, não depende da variável x, podendo esta ser trocada por qualquer outra variável sem a alteração do valor da integral.
Para se calcular uma integral definida, podemos utilizar a sua definição, porém esse método requer certo conhecimento com somatório e limites, já que a definição abrange ambos. Podemos também utilizar as tabelas de integrais que são encontradas em livros didáticos ou mesmo na internet.
Serão mostrados, a seguir, alguns exemplos para que você possa compreender como se calcula uma integral definida a partir da tabela de integrais.

Nos exemplos acima, foi utilizada a forma da integral de polinômio e da integral do seno. Para resolver, substituímos os valores dos limites superiores e inferiores no resultado da integral. Em seguida, fazemos o resultado do limite superior menos o resultado do limite inferior.
Integral indefinida
De forma geral, a integral indefinida de uma função f é conhecida como sendo a primitiva de f. Em outras palavras, a integral indefinida representa toda uma família de funções que são diferenciadas por uma constante C. Alguns exemplos de integral indefinida:
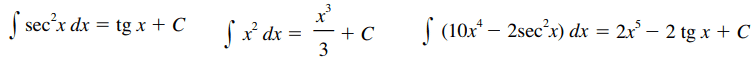
Enquanto a integral definida é um número – por exemplo, o valor da área de um gráfico -, a integral definida é uma função.
O cálculo desse tipo de integral também é feito através da tabela de integrais que foi citada anteriormente. Um exemplo dessa tabela pode ser visto a seguir.
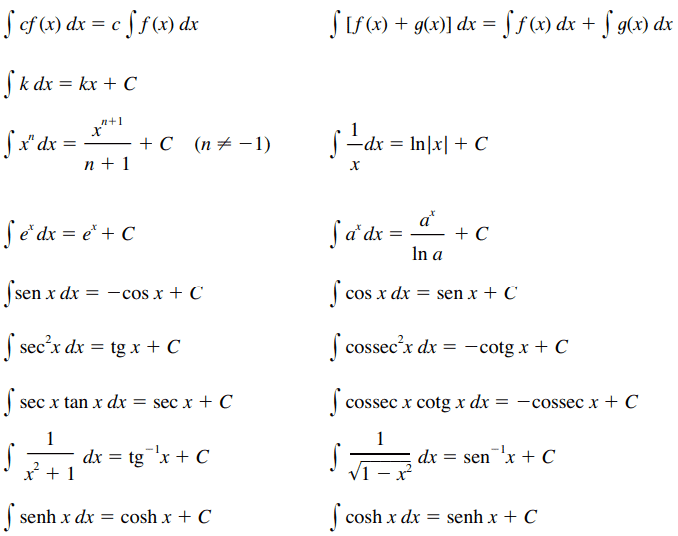
Saiba mais sobre integrais
A seguir, confira algumas videoaulas sobre integrais para que você possa entender mais sobre elas e tirar as suas dúvidas restantes sobre o assunto!
Noções básicas
Aqui, são mostrados alguns dos conceitos básicos sobre integrais. Dessa forma, quase todo o conteúdo visto acima pode ser revisado com essa videoaula.
Integral indefinida
Nesse vídeo, é apresentada uma introdução sobre as integrais indefinidas e algumas de suas propriedades. Acompanhe!
Integral definida
Entender sobre integral definida é muito importante, pois ela tem várias aplicações. Pensando nisso, confira aqui uma breve aula sobre essa integral e o cálculo de áreas.
Por fim, é importante revisar também sobre funções e derivadas. Dessa forma, seus estudos vão ficar completos!
Referências
Cálculo – volume I (2013) – James Stewart

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Integrais. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/integrais. Acesso em: 03 de April de 2025.
1.
Calcule a seguinte integral definida:
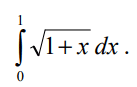
Solução
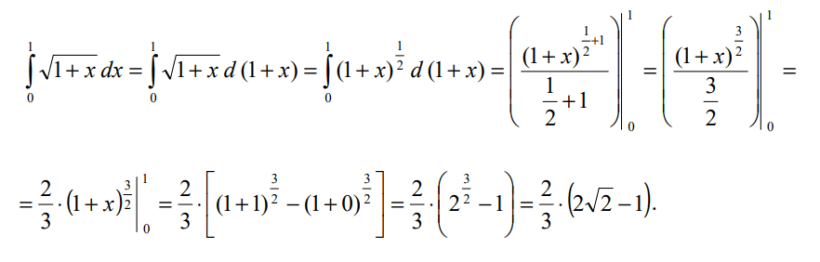
2.
Calcule a seguinte integral definida:
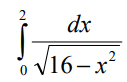
Solução: