Função Linear

A matemática está presente em muitos momentos de nossas vidas, desde os preços de uma feira, uma corrida ao ar livre, crescimento de uma população. Em suma, podemos encontrar a matemática em muitos ambientes.

Publicidade

Dessa forma, estudaremos aqui uma função muito importante para a matemática e o nosso cotidiano. Conhecida como função afim ou função linear, é uma função que representa o crescimento ou decrescimento, de uma maneira “reta” ou “linear”, de algo estudado.

Domínio, contradomínio e imagem de uma função

Uma propriedade importante de se conhecer, antes de entrarmos na definição de uma função linear, é o domínio, contradomínio e imagem de uma função. Desde já, vamos então ver a definição dessas propriedades:

Dada uma função f de A em B, o conjunto A chama-se domínio (D) da função e o conjunto B, contradomínio (CD) da função. Para cada x ϵA, o elemento y ϵB chama-se imagem de x pela função f ou o valor assumido pela função f para x ϵA, e o representamos por f(x). Assim, y = f(x).

O que é uma função linear

Antes de mais nada, suponha a seguinte situação: mensalmente, um representante comercial recebe um salário de R$ 2500,00 e mais uma comissão de 6% sobre o total das vendas que realiza durante o mês.

De acordo com as condições apresentadas, podemos expressar o salário do representante comercial da seguinte forma: salário mensal = 2500 + 0,06 x (total das vendas do mês).

Esse salário, segundo apresentado acima, é dado em função do total de vendas feitas durante todo o mês. Dessa forma, uma função linear pode ser definida da seguinte maneira:

Publicidade

Uma função R⟶ R chama-se função afim quando existem dois números reais a e b tal que f(x)=ax+b para todo x∈R.
Ela é chamada de função linear quando b=0, assim, uma função linear é do tipo f(x)=ax.

Gráfico de uma função linear

Uma função inversa, função exponencial e entre tantas outras podem ser representadas por um gráfico. A função linear também pode ser representada por um gráfico com suas propriedades particulares, confira:

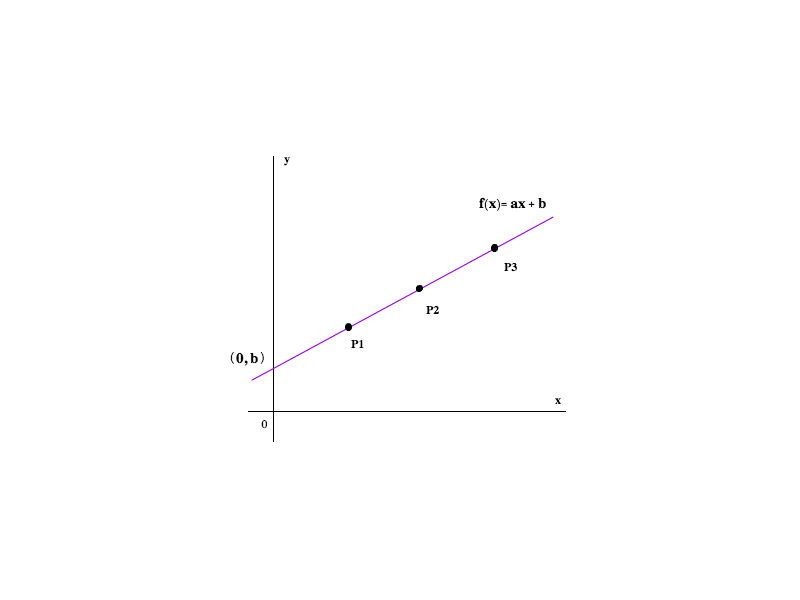
A partir do gráfico, observa-se algumas propriedades específicas desse tipo de função. Geometricamente, a constante b de uma função f(x)=ax+b é o ponto onde a reta intersecta o eixo y.

Publicidade

Sob o mesmo ponto de vista, o número a é conhecido como coeficiente angular da reta em relação ao eixo x, ou seja, a determina a declividade da reta.

Com uma breve noção do gráfico de uma função linear, em síntese, temos a capacidade de entender dois tipos de funções lineares diferentes: função crescente e função decrescente.

Função crescente e decrescente

Tomando novamente o exemplo do representante comercial, posteriormente mencionado, o salário dele nunca decrescera, pois não existe a possibilidade de vendas negativas durante o mês. O mínimo permitido seria zero vendas.

Da mesma forma, suponha agora que há uma piscina cheia de água e uma pessoa deseja esvaziá-la. Para isso, a pessoa abre uma tampa que libera a água dessa piscina de uma maneira linear. O volume dessa piscina está decrescendo com o tempo.

Dessa forma, podemos introduzir o conceito de uma função crescente e uma função decrescente.

Função crescente

Uma função linear crescente ocorre quando o coeficiente angular for positivo, ou seja, a ≥ 0. Nesse caso, temos a=3, portanto a função é crescente.

Função decrescente

A função linear é decrescente quando o seu coeficiente angular é menor do que zero, dessa forma, temos que a<0. Segundo essa definição, o gráfico apresentado posteriormente se refere a uma função decrescente, pois a=-2.

Essas definições de funções lineares crescentes ou decrescentes são de muita importância na resolução de exercícios, sendo dessa forma, o ideal entendimento desse assunto.

Entenda mais sobre função linear

Além dos assuntos abordados até aqui, confira alguns vídeos que tratam do assunto e vão complementar seus estudos:

O que é função linear

O vídeo explica, de uma maneira bem didática, a definição de uma função linear e alguns exemplos dessa função.

Gráficos da função linear

Da mesma forma, nesse vídeo explica-se os gráficos de uma função linear.

O crescimento da economia, do salário de um trabalhador entre outras coisas cotidianas podem ser representados por essa função, o que fazem dela um conteúdo bem comum em questões de vestibulares e exames.

Referências