Uma função pode ser definida de várias formas, dependendo de como o seu conjunto domínio se relaciona com o conjunto do contradomínio. Assim, podemos identificar se uma função é injetora, sobrejetora ou bijetora.
Publicidade
Dessa forma, estudaremos alguns conceitos sobre a função injetora. Conheceremos o domínio e o contra domínio dessa função, além de observamos o gráfico, alguns exemplos e resolver exercícios.
O que é uma função injetora
Antes de mais nada, vamos entender um pouco mais sobre o que é um domínio e um contradomínio de uma função.
O domínio de uma função é o conjunto de “entrada”, ou seja, é o conjunto que define a função. Por outro lado, o contradomínio é o conjunto de “chegada”, assim, é o conjunto que contém todas as possíveis imagens da função.
Relacionadas
.
Quando os elementos de um conjunto domínio de uma função qualquer se relacionam com elementos distintos do contradomínio dessa função, ela pode ser chamada de função injetora ou função injetiva.
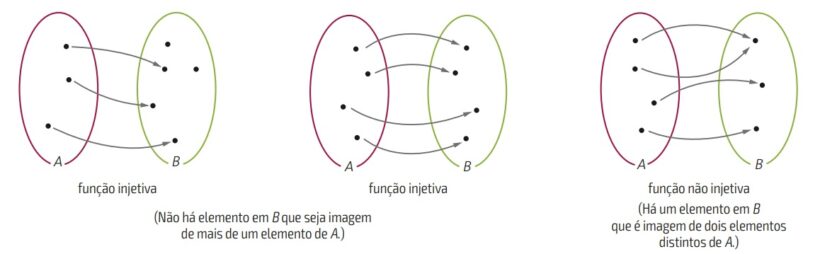
Isso pode ser observado na figura a seguir:
Publicidade
Nas duas primeiras imagens podemos observar que existem elementos distintos do conjunto A (domínio) que se relacionam com elementos distintos do conjunto B (contradomínio), caracterizando assim uma função injetora.
Porém, na ultima representação observamos que dois elementos do domínio se relacionam com um mesmo elemento do contradomínio, nesse caso essa função não é injetora.
De uma maneira mais formal, podemos definir uma função injetora da seguinte maneira:
Publicidade
Sejam A e B o domínio e contradomínio, respectivamente, de uma função f. Então f é injetora quando: x1 ≠ x2 em A ⇒ f(x1) ≠ f(x2) em B.
Gráfico de uma função injetora
Em certas situações, principalmente em exercícios que envolvam uma função injetora, existem gráficos a respeito dessas funções. Dessa forma, podemos identificar esse tipo de função a partir do gráfico com um simples “macete”.
Pela definição de uma função injetora, não existe elementos do contradomínio que se relacionam com dois elementos do domínio ao mesmo tempo. Logo, se traçarmos linhas horizontais cortando o gráfico e elas cruzarem o gráfico em apenas um ponto, então a função é injetora.
Assim, conforme o gráfico a seguir, podemos entender um pouco mais esse “macete”.
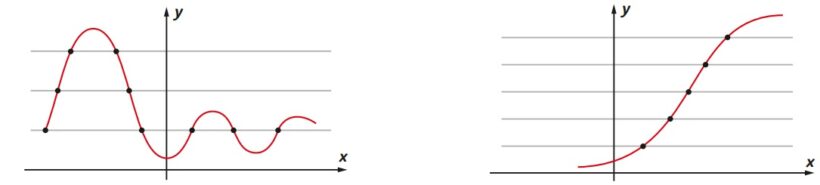
Na imagem acima, podemos observar que o gráfico da esquerda é de uma função não injetora, pois as retas horizontais traçadas no gráfico tocam mais de um ponto.
Por outro lado, o gráfico da direita é de uma função injetora, já que as retas horizontais tocam em apenas um ponto do gráfico.
Esse “macete” facilita a resolução de determinados exercícios, pois nos economizam tempo.
Exemplos de função injetora
Com a definição em mente, precisamos nos perguntar: “como eu sei se uma função é ou não injetora?”. A partir de alguns exemplos, que serão apresentados a seguir, conseguiremos obter a resposta para tal pergunta.
Função quadrática qualquer
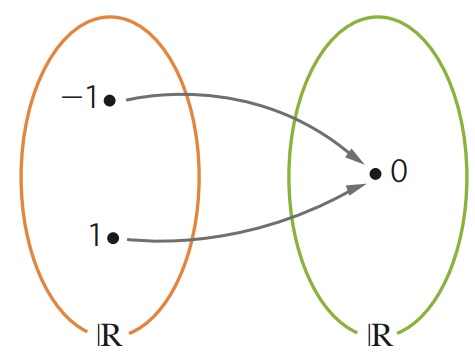
Seja f definida como f:|R ⇒ |R e dada por f(x) = x2 – 1. Ela não é injetiva, pois:
- para x = 1, temos que f(1) = 0;
- e para x = -1 temos que f(-1) = 0.
Dessa forma, temos um mesmo elemento do domínio que corresponde a uma mesma imagem no contradomínio.
Função “dobro”
Quando queremos saber o dobro de um número, precisamos apenas multiplicar esse número por 2. Assim, podemos definir uma função dobro da seguinte forma: Seja f definida como f:|R ⇒ |R e dada por f(x) = 2x.
Essa função é injetora, pois a cada número real x essa função corresponde ao seu dobro 2x. Não existe dois números reais com o mesmo dobro. Simbolicamente, temos que: Para quaisquer x1,x2∈R, x1 ≠ x2 ⇒ 2x1 ≠ 2x2 ⇒ f(x1) ≠ f(x2).
Existem muitas outras funções injetoras e não injetoras, mas apenas com a prática conseguiremos saber diferenciar essas funções.
Entenda mais sobre função injetora
Por fim, podemos entender um pouco mais sobre essa função a partir de vídeos explicativos sobre o assunto. A seguir apresentamos alguns:
Definição de função injetora e seu gráfico
Neste vídeo são apresentados o conceito e definição de uma função inversa, além de apresentar também sobre o “macete” dos gráficos dessa função.
Assunto do vídeo
Para o caso desse vídeo, podemos entender um pouco mais como são aplicadas as definições de função injetora e sobrejetora em um exercício.
As funções injetoras são de extrema importância para o entendimento de um outro tipo de função, que seria a função bijetora. Porém, esse assunto será tratado em um outro momento.
Referências
Matemática: ciência e aplicações – Gelson Iezzi;
Matemática: contexto & aplicações – Luiz Roberto Dante.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Função injetora. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcao-injetora. Acesso em: 04 de April de 2025.
1.
Verifique que f(x) = 2x + 1 é uma função injetora no conjunto dos números reais.
Suponha que x1 = 1 e x2 = 3. Assim, teremos a seguinte situação
f(1) = 2.1 + 1 = 3
f(3) = 2.3 + 1 = 7
Portanto, como a função relaciona apenas um elemento do contradomínio com seu domínio, então a função é injetora.
2. [Unifesp]
Há funções y = f(x) que possuem a seguinte propriedade: “a valores distintos de x correspondem valores distintos de y”. Tais funções são chamadas injetoras. Qual, dentre as funções cujos gráficos aparecem abaixo, é injetora?
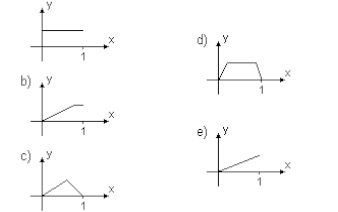
Traçando retas horizontais em todos os gráficos, apenas o gráfico da alternativa e) não toca em dois pontos ao mesmo tempo. Isso quer dizer que o contradomínio da função do gráfico corresponde a elementos distintos do domínio.
RESPOSTA: e)