Já está acostumado a resolver equações de primeiro e de segundo graus? Neste post, você vai aprender como resolver equações nas quais a incógnita está localizada no expoente e a base é um número real positivo diferente de 1: a equação exponencial. Acompanhe!
Publicidade
O que é equação exponencial
Para ser considerada uma equação, a expressão algébrica deve conter ao menos uma incógnita e uma igualdade. Uma equação exponencial deve apresentar a incógnita em um expoente, na qual as bases devem ser números reais positivos diferentes de 1. Ou seja, deve ser da seguinte forma:
Relacionadas
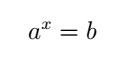
Note que a e b são números reais e x deve ser positivo e diferente de 1.
Propriedades da equação exponencial
Para resolver equações exponenciais, é preciso obter potências de mesma base. Para isso, é necessário relembrar algumas propriedades da potenciação, as quais ajudarão nas resoluções. Acompanhe:
- Multiplicação de potências de mesma base: repete-se a base e somam-se os expoentes.
- Divisão de potências de mesma base: repete-se a base e subtraem-se os expoentes.
- Potência de potência: repete-se a base e multiplicam-se os expoentes.
- Potência do produto: a potência do produto é o produto das potências.
- Potência do quociente: a potência do quociente é o quociente das potências.
- Potência negativa: inverte-se a base e o expoente passa a ser positivo, desde que o denominador seja diferente de zero.
- Potência fracionária: quando o expoente é uma fração, pode-se escrever a operação na forma de radical. Assim, o denominador do expoente passa a ser o índice do radical, enquanto o numerador do expoente passa a ser o expoente do radicando.
- Igualdade de potências de mesma base: se duas potenciações têm a mesma base e são iguais, isso implica que os seus expoentes também sejam iguais.
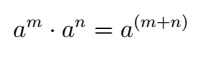
Publicidade
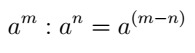
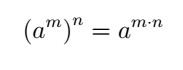
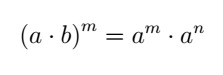
Publicidade
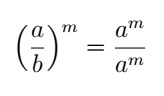
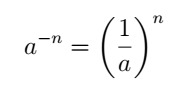
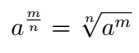
![]()
Essas são as principais propriedades da potenciação, as quais serão úteis na resolução de uma equação exponencial.
Resolução de equação exponencial
Para resolver uma equação exponencial, é preciso organizar a expressão algébrica de modo a obter uma igualdade de potências com a mesma base.
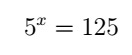
Nesse caso, é fácil perceber que 125 equivale a 53. Assim:
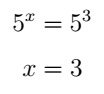
Com base em uma das propriedades da potenciação, obtemos que x = 3. Ou seja, se 5x= 53, podemos afirmar que x = 3.
Vídeos sobre equações exponenciais
Existem várias outras abordagens para a resolução de problemas que envolvam equações exponenciais. As videoaulas abaixo vão te ajudar a aprofundar ainda mais seu conhecimento desse assunto. Confira:
Equações exponenciais com bases diferentes
Como resolver equações exponenciais quando as bases são diferentes? Para isso, é necessário aplicar as propriedades dos logaritmos. Para aprender a resolver esse tipo de equação, veja o vídeo do professor Grings!
Resolução comentada de uma equação exponencial
Aqui, o professor Robson Liers resolve um exercício que envolve soma de potências e equações exponenciais. Esse tipo de expressão algébrica é muito cobrado em provas de grande escala, como Enem e vestibulares.
Função exponencial e equação exponencial
De que maneira a função exponencial se relaciona com a equação exponencial? Veja o vídeo do professor Ferretto para compreender melhor a relação entre esses dois conceitos matemáticos.
Para resolver todos os tipos de equação exponencial, que tal conferir também este conteúdo sobre logaritmos? Aproveite para aprender mais e bons estudos!
Referências
Pré-Calculo (2013) – Franklin D. Demana et al.
Um Curso de Cálculo – Volume 1 (2001) – Hamilton Luiz Guidorizzi

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Equação exponencial. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/equacao-exponencial. Acesso em: 18 de April de 2025.
1. [Mackenzie]
A soma das raízes da equação (4x)2x-1 = 64 é igual a:
a) -1/2
b) -1
c) 1/2
d) 1
e) 52
Aplicando as propriedades da potenciação, temos que:
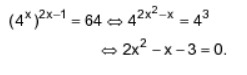
Encontrando as raízes para a equação de segundo grau, obtemos: x’ = 3/2 e x” = -1.
Ao somar as duas raízes, encontramos o valor de 1/2.
Resposta correta: C
2. [Unesp]
Admita que o número de visitas diárias a um site seja expresso pela potência 4n, com n sendo o índice de visitas ao site. Se o site S possui o dobro de visitas diárias do que um site que tem índice de visitas igual a 6, o índice de visitas do site S é igual a:
a) 12
b) 9
c) 8,5
d) 8
e) 6,5
Sendo x o índice de visitas ao site S, temos:
4x = 2 · 46
Como 2 equivale à raiz quadrada de 4, podemos escrevê-lo como 41/2 = 40,5.
Assim,
4x = 40,5 · 46
Temos uma multiplicação de potências com a mesma base. Assim, repetimos a base e somamos os expoentes.
4x = 46,5
Como as bases são iguais, concluímos que x = 6,5.
Resposta correta: E