À primeira vista, uma casquinha de sorvete é apenas uma casquinha de sorvete, certo? Para a matemática, porém, existe outra definição para essa guloseima.
Publicidade
Conhecemos a casquinha de sorvete como a forma geométrica chamada cone, sendo essa muito importante para a definição de várias outras curvas conhecidas como cônicas: a elipse, a parábola, a hipérbole e a circunferência.
Cone duplo de revolução

Relacionadas
As cônicas são geradas a partir do cone duplo de revolução, uma figura obtida da rotação de um triângulo retângulo em volta de um dos seus catetos.
A partir da interseção de um plano com o cone de revolução dupla, podemos obter as quatros curvas citadas acima: circunferência, elipse, parábola e hipérbole. A diferença entre elas está no modo em como o plano “corta” o cone.
Circunferência
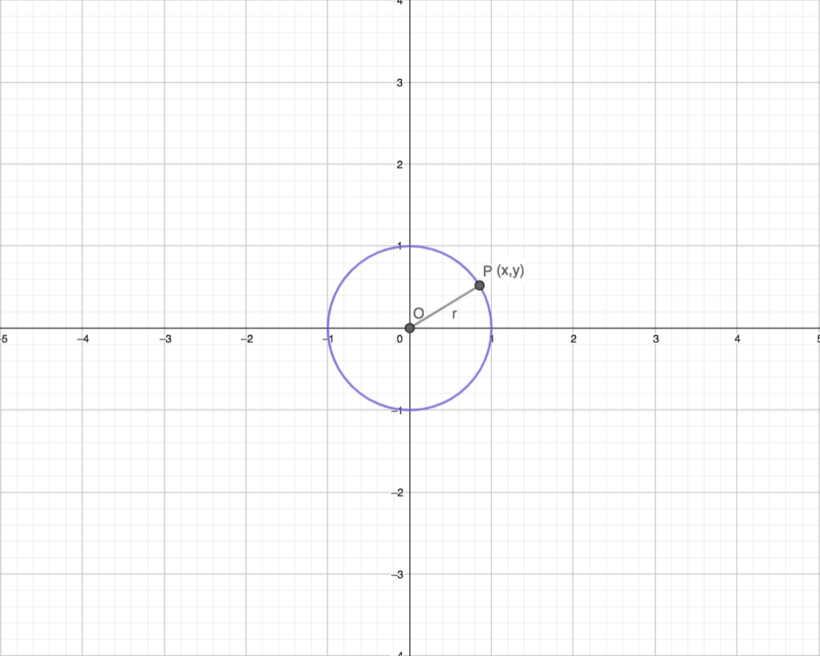
Sendo,
- O: centro da circunferência
- r: raio da circunferência
Uma circunferência de centro O (a, b) e raio r é o conjunto de todos os pontos P (x, y), cujo a distância até o centro é sempre o raio r.
Publicidade
Equação
Juntamente com a definição, podemos obter a equação reduzida da circunferência, escrita da seguinte forma:
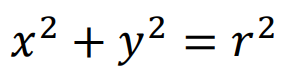
Elipse
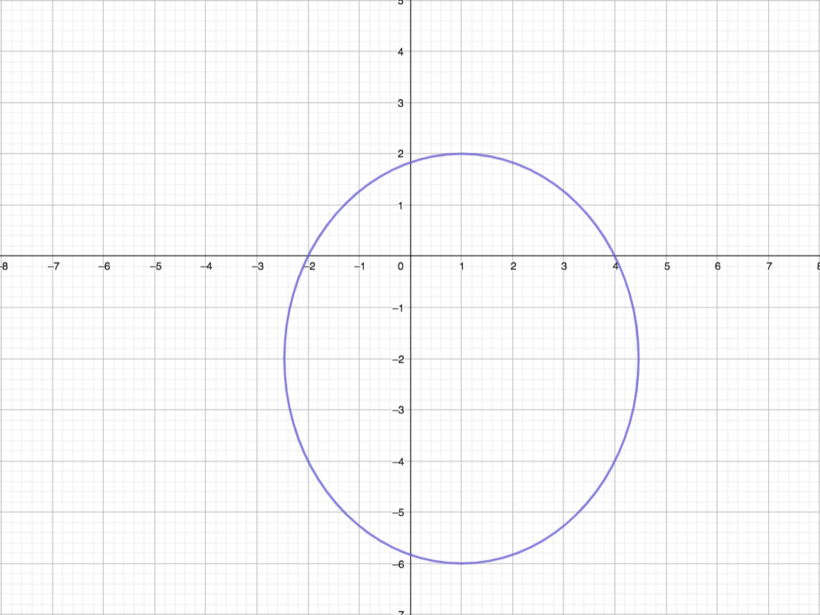
Sendo,
- F1 e F2: focos da elipse e a distância entre eles é a distância focal (2c);
- A1A2: eixo maior da elipse, cuja medida é 2a;
- B1B2: eixo menor da elipse, cuja medida é 2b;
- O: centro da elipse, intersecção dos eixos da elipse e ponto médio dos eixos;
- e: excentricidade da elipse se e = c/a.
Quando um cone é cortado por um plano inclinado e que corte todas suas geratrizes, obtemos uma secção cônica chamada de elipse. O plano não pode ser paralelo ao plano da base, pois neste caso obteríamos uma circunferência. Dessa forma, as equações reduzidas da elipse podem ser deduzidas a partir da distância entre pontos.
Publicidade
Equações
Em suma, quando a elipse está no centro de coordenadas do plano cartesiano, e seu eixo maior está em x, temos a seguinte equação, conhecida como equação reduzida da elipse:
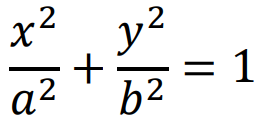
Por outro lado, quando a elipse está fora do centro do plano cartesiano, temos a seguinte equação:
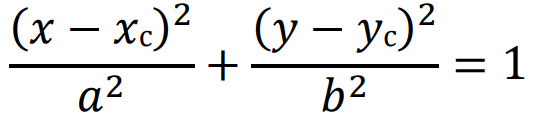
* Em que, xc e yc são o centro da elipse
Parábola
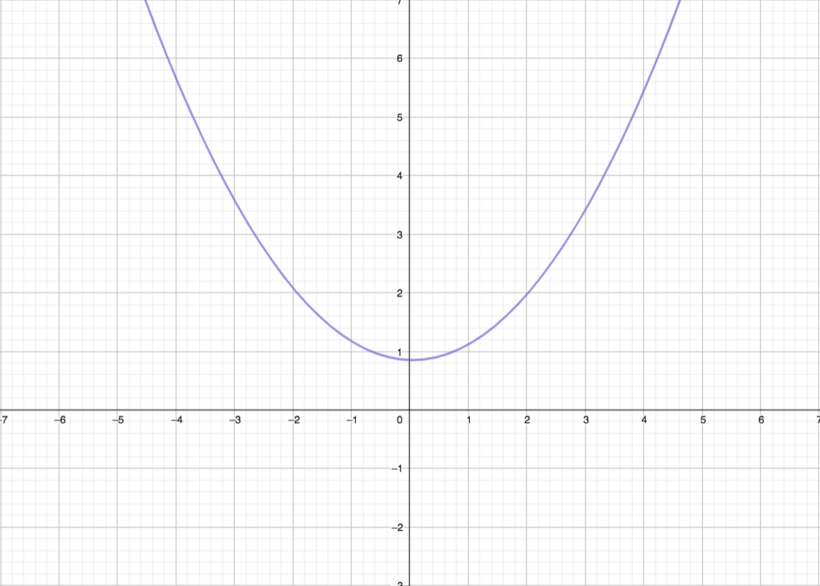
Sendo,
- F: foco da parábola;
- d: diretriz da parábola;
- V: vértice da parábola;
- Eixo de simetria: reta que passa por F e é perpendicular a d;;
Teremos então duas equações para a parábola.
Equações
A primeira equação tem simetria vertical, ou seja, a reta diretriz é em x.
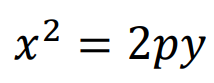
Ainda mais, a segunda equação se faz presente quando a parábola está fora do centro do plano, sendo sua equação:
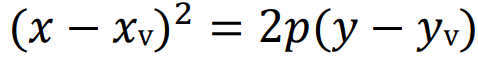
ainda mais, temos que xv e yv é o vértice da parábola. Se xv = 0 e yv = 0, voltamos a primeira equação reduzida da parábola.
Hipérbole
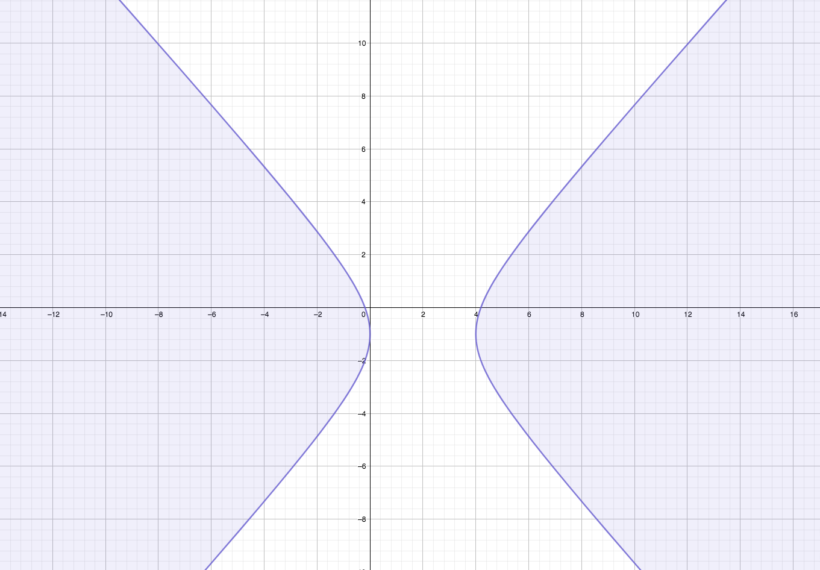
Sendo,
- F1 e F2: focos da hipérbole, em que F1 F2 = 2c a distância focal;
- A1 e A2: vértices da hipérbole
- O: centro da hipérbole.
- e: excentricidade da hipérbole, em que e = c/a.
Dessa forma, podemos montar as equações da hipérbole.
Equações
A primeira equação reduzida da hipérbole é obtida quando os focos estão sobre o eixo x:
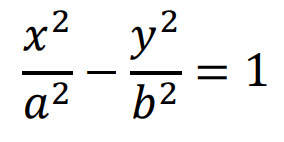
A segunda equação se deve ao fato de que a hipérbole está fora do centro do plano cartesiano, ficando:
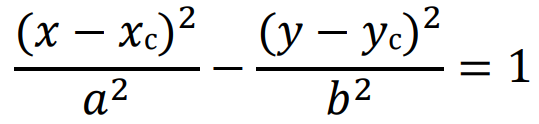
* Em que, xc e yc são o centro da hipérbole
Resumo
Para fechar, assista a seguir um vídeo que resume as cônicas estudadas:
Referências
Matemática: contexto & aplicações – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Cônicas. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/conicas. Acesso em: 29 de April de 2025.
1. [IFB – 2017]
Considerando uma elipse com centro na origem, focos num dos eixos coordenados e passando pelos pontos (5, 0) e (0, 13), determine os focos da elipse.
a) (13, 0) e (– 13, 0)
b) (0, 13) e (0, – 13)
c) (12, 0) e (– 12, 0)
d) (0, 12) e (0, – 12)
e) (5, 0) e (– 5, 0)
Sabemos que, para toda elipse, vale a relação a2 = b2 + c2, sendo 2a a distância do eixo maior, 2b a distância do eixo menor e 2c a distância entre os focos da elipse.
Pelo enunciado da questão, temos que a = 13 e b = 5, dessa forma, podemos substituir na relação a2 = b2 + c2. Logo, temos que
132 = 52 + c2
Elevando 13 e 5 ao quadrado, obtemos que
169 = 25 + c2
Isolando c da equação a cima, temos
c2 = 169 – 25
Dessa forma
c2 = 144
Tirando a raiz quadrado de ambos os lados, obtemos que
c = 12
Portanto, os focos da elipse são (0,12) e (0,-12).
Resposta: D
2. [Petrobrás – Cesgranrio 2010]
Os vértices imaginários da hipérbole da equação abaixo são:
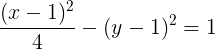
a) (2,1) e (2,3)
b) (2,0) e (2,2)
c) (2,0) e (1,2)
d) (1,1) e (1,2)
e) (1,0) e (1,2)
Vamos começar identificando os dados da hipérbole. Pelas informações da equação do exercício, o centro é (1,1), a = 2 e b = 1. Com isso, podemos desenhar a hipérbole que pode ser vista na figura a seguir
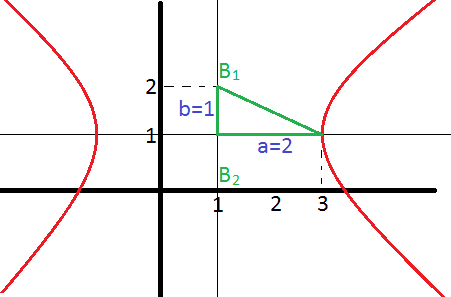
Dessa forma, temos que os eixos imaginários B1 e B2 são (1,0) e (1,2).
Resposta: e