Na matemática costumamos aprender sobre a área das figuras planas. Dentre elas, encontramoso trapézio, que tem sua área bastante relacionada à área do triângulo. Um trapézio, é um quadrilátero plano convexo que possui dois lados paralelos, que são chamados de bases. Estas são sempre diferentes, de forma que, como regra, terão uma base menor e uma base maior. A distância entre essas duas bases, é chamada de altura do trapézio. Para calcular a área de um triângulo, nós usamos a fórmula A = b . h / 2, onde A é a área, b é a base e h é a altura do triângulo.
Publicidade
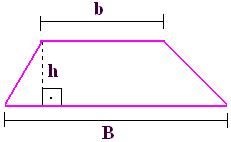
O trapézio é formado por uma base maior, normalmente representada por B, uma base menor, representada comumente por b, e uma altura, que assim como no caso do triângulo, é representada por h. Quando vamos calcular a área de um trapézio, podemos facilitar dividindo-o em dois triângulos, como representado nas imagens a seguir:
Nesta primeira imagem, estamos completando as alturas do trapézio.
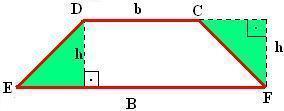
Na segunda, estamos dividindo-o em dois triângulos.
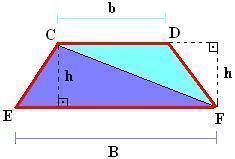
Dessa forma, podemos calcular a área do trapézio somando as áreas dos dois triângulos ∆CFD e ∆CEF. Assim, basta aplicarmos a fórmula do cálculo da área do triângulo nos dois, da seguinte forma:
A∆1 = B . h / 2
A∆2 = B . h / 2
Publicidade
Somando, temos a fórmula usada para calcular a área de qualquer trapézio, confira:
AT = A∆1 + A∆2
AT = B . h / 2 + b . h / 2
AT = B. h + b . h / 2
AT = h (B + b) / 2
Temos, portanto, que a fórmula para o cálculo do trapézio é:
Publicidade
A = h (B + b) / 2
Classificação dos trapézios
Os trapézios são classificados de acordo com os lados que não são bases, seguindo as seguintes regras:
São isóceles quando os lados que não são as bases são congruentes (ou seja, são iguais);
São Escalenos quando os lados que não são bases são não congruentes, ou seja, não são iguais;
São retângulos quando possuem dois ângulos retos, ou seja, dois ângulos de 90°.
Referências
http://www.unesp.br/prograd/PDFNE2005/artigos/capitulo%205/ensinandoarea.pdf
http://server09.obmep.org.br/docs/apostila3.pdf

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Área do Trapézio. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/area-do-trapezio. Acesso em: 25 de April de 2025.
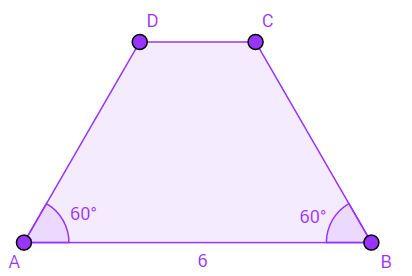
01. [FGV] Na figura, AB = CD, AB = 6 cm, AD = 4 cm e os ângulos internos de vértices A e B têm as medidas indicadas. A área do quadrilátero ABCD, em centímetros quadrados, é:
a) √3
b) 2√3
c) 4√3
d) 6√3
e) 8√3
02. [UFPE] A área do trapézio (figura abaixo) é igual a
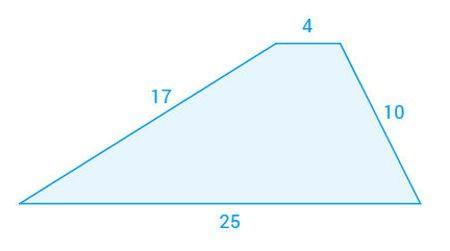
a) 86
b) 96
c) 106
d) 116
e) 126
01. [Para calcular a área de um trapézio, precisamos das medidas de suas bases e de sua altura. Então, nesse exercício, calcularemos a altura (h), a base menor (b) e, depois, a área (A).
A altura pode ser obtida por meio do seno do ângulo de 60º. Observe que, desenhando a altura desse trapézio, partindo do vértice D para a base AB, forma-se um triângulo.
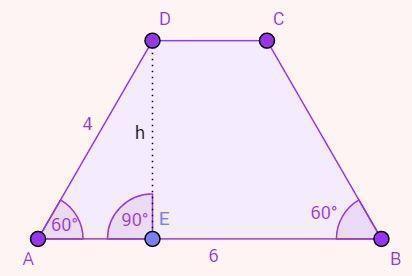
Sen 60º = h
4
√3 = h
2 4
h = 4√3
2
h = 2√3
Para encontrar o valor da base menor, precisamos descobrir os valores dos segmentos AE e BF, também desenhados sobre esse mesmo trapézio:

Esse problema resume-se a calcular o valor de y, que é o mesmo dos dois lados do trapézio, pois AB = CB (dado do exercício). Para isso, usaremos cosseno:
Cos 60º = y
4
1 = y
2 4
y = 4
2
y = 2
Observe que a base menor é justamente o comprimento do segmento EF, ou seja, 6 – 2y. Portanto, a base menor mede 2.
Para finalizar o exercício, basta calcular a área do trapézio:
A = (B + b) · h
2
A = (6 + 2) · 2√3
2
A = 8 · 2√3
2
A = 8√3
Resposta: letra E]
02. [Para calcular a área desse trapézio, precisamos encontrar sua altura. Essa tarefa só será possível por meio de ideias de sistemas de equações. Acompanhe:
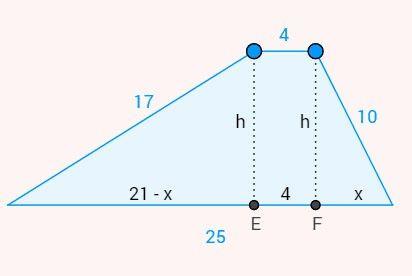
Utilizando o teorema de Pitágoras, teremos dois valores para h2. Observe:
Primeiro valor:
h2 + x2 = 102
h2 = 102 – x2
Segundo valor:
h2 + (21 – x)2 = 172
h2 = 172 – (21 – x)2
Igualando esses valores, teremos:
102 – x2 = 172 – (21 – x)2
100 – x2 = 289 – (212 – 2·21·x + x2)
100 – x2 = 289 – 441 + 42·x – x2
100 – 289 + 441 = 42·x
252 = 42·x
x = 252
42
x = 6
Utilize o valor de x para descobrir a altura por meio do teorema de Pitágoras:
h2 + x2 = 102
h2 + 62 = 102
h2 + 36 = 100
h2 = 100 – 36
h2 = 64
h = 8
Agora calcule a área do trapézio:
A = (B +b)·h
2
A = (25 + 4) · 8
2
A = 29 · 4
A = 116
Resposta: letra D]