Sabemos que tanto os materiais sólidos quanto a atmosfera exercem pressão na superfície dos corpos com que entram em contato. É natural, então, que o mesmo efeito ocorra com os líquidos. Dessa forma, vamos estudar aqui o teorema de Stevin, o teorema de Pascal e os vasos comunicantes.
Publicidade
Teorema de Stevin
Suponha que um mergulhador esteja na superfície da água, pronto para começar a mergulhar. Nessa situação, ele sente uma leve pressão no seu corpo. Ele então começa a mergulhar e ir cada vez mais fundo. Quanto mais ele mergulhar, mais ele vai sentindo a pressão em seu corpo.
Em outras palavras, quanto maior for o desnível do mergulhador citado anteriormente, maior será a variação de pressão. Isso serve para qualquer corpo. Este é o enunciado do Teorema de Stevin. De uma maneira mais formal:
Relacionadas
A diferença entre as pressões (Llp) de dois pontos, em um fluido em equilíbrio, é calculada pelo produto entre a densidade do fluido, a aceleração gravitacional e o desnível (Llh) entre as profundidades dos pontos:
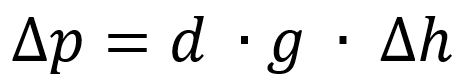
Na equação acima temos, de uma forma matemática, como a pressão varia em função da densidade do líquido (d), da aceleração da gravidade (g) e da variação da altura (∆h).
Teorema de Pascal
No momento em que uma injeção, por exemplo, é aplicada no braço de uma pessoa, o acréscimo de pressão exercida na superfície das partículas do medicamento líquido, dentro do êmbolo, transmite-se através das demais e ultrapassa a extremidade da agulha. Em outras palavras, a pressão é transmitida igualmente por todo o líquido.
Publicidade
Essa transmissão foi descrita pela primeira vez por Blaise Pascal. Assim, o teorema que leva o seu nome é descrito da seguinte forma:
Quando um ponto de um líquido em equilíbrio sofre variação de pressão, acontece o mesmo com os demais pontos dele, em igual intensidade.
Esse teorema é importante para o entendimento sobre os vasos comunicantes.
Publicidade
Vasos comunicantes
Se dois ou mais recipientes forem interligados por um tubo, consideramos esse sistema como sendo um vaso comunicante.
Esse sistema é utilizado para o estudo de pressão exercido por líquidos e a relação entre as densidades de líquidos imiscíveis.
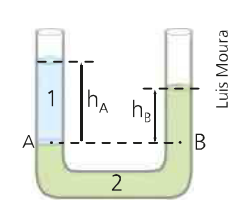
Um grande exemplo prático de vasos comunicantes são as prensas hidráulicas, que são dispositivos multiplicadores de intensidade de força.
Saiba mais sobre o teorema de Stevin
Para que nenhuma dúvida fique para trás, apresentaremos a você alguns vídeos a respeito do assunto estudado até aqui.
Conceitos sobre o Teorema de Stevin
Revise e entenda mais sobre os conceitos sobre o Teorema de Stevin. Assim não fica nenhuma dúvida sobre o assunto estudado!
Vasos comunicantes
Os vasos comunicantes são importantes para o entendimento desse assunto. Dessa maneira, esse vídeo irá te ajudar a entender como se aplicar o tema sobre vasos comunicantes.
Exercício resolvido
Exercício resolvido é importante para a fixação das equações e o seu entendimento. Dessa forma você irá fazer bonito na hora da prova!
E para finalizar, veja a seguir alguns exercícios para você colocar em prática seus conhecimentos sobre o que foi estudado até aqui.
Referências
Física para o ensino médio, vol. 1: mecânica – Kazuhito Yamamoto;
As faces da física – Wilson Carron.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Teorema de Stevin. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/teorema-de-stevin. Acesso em: 02 de April de 2025.
1. [ENEM]
O manual que acompanha uma ducha higiênica informa que a pressão mínima da água para o seu funcionamento apropriado é de 20 kPa. A figura mostra a instalação hidráulica com a caixa d’água e o cano ao qual deve ser conectada a ducha.
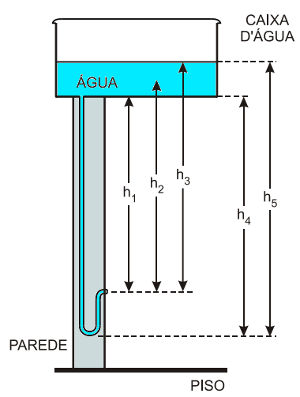
O valor da pressão da água na ducha está associado à altura
a) h1
b) h2
c) h3
d) h4
e) h5
De acordo com a lei de Stevin, a pressão gerada por uma coluna de líquido depende da altura dessa coluna. Sendo assim, a partir do ponto onde está a ducha, a altura relacionada com a pressão é h3.
RESPOSTA: c)
2. [UNESP]
A diferença de pressão máxima que o pulmão de um ser humano pode gerar por inspiração é em torno de 0,1 x 105 . Pa ou 0,1 atm. Assim, mesmo com a ajuda de um snorkel (respiradouro), um mergulhador não pode ultrapassar uma profundidade máxima, já que a pressão sobre os pulmões aumenta à medida que ele mergulha mais fundo, impedindo-os de inflarem.
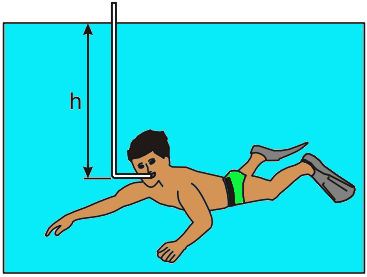
Considerando a densidade da água ρ ≅103 kg/m e a aceleração da gravidade g ≅ 10 m/s2, a profundidade máxima estimada, representada por h, que uma pessoa pode mergulhar respirando com a ajuda de um snorkel é igual a
a) 1,1.102 m
b) 1,0.102 m
c) 1,1.101 m
d) 1,0.101 m
e) 1,0.100 m
A diferença de pressão (Δp) pode ser dada pela lei de Stevin:
Δp = ρ . g . h
Substituindo os valores, temos que:
0,1 x 105 = 103 . 10 . h
1 x 104 = 104 . h
h = 1m = 1,0 x 100 m