Sabemos que um carro em movimento não mantém a mesma velocidade durante todo o trajeto. Ora ele anda mais rápido, ora reduz a velocidade e também, em outros momentos, permanece em repouso. A isso damos o nome de movimento uniformemente variado (MUV). Estudaremos aqui o que é esse movimento, suas definições e exemplos.
Publicidade
O que é movimento uniformemente variado?
Antes de mais nada, é necessário o entendimento sobre o que é a aceleração de um corpo.
Aceleração
No domínio da Física, acelerar é fazer a intensidade (valor) e/ou direção e/ou sentido da velocidade do móvel se alterar. Isso pode ser feito tanto aumentando quanto diminuindo a velocidade.
Relacionadas
Quando o módulo da velocidade aumenta, dizemos que o movimento é acelerado. Caso contrário, quando a velocidade perde valor do seu módulo, o movimento é chamado de retardado.
Além disso, é possível definir a aceleração como aceleração escalar média ou instantânea. A primeira é denominada como a variação da velocidade de um móvel em um determinado intervalo de tempo. A equação para a aceleração escalar média é:
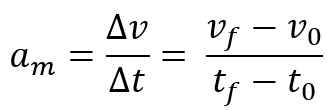
Quando tomamos a aceleração escalar média em um intervalo de tempo muito pequeno, ou seja, quase zero, chamamos essa aceleração de instantânea ou, simplesmente, o valor da aceleração em um determinado instante.
Publicidade
Movimento uniformemente variado
Com a ideia de aceleração em mente, podemos agora entender os conceitos do movimento uniformemente variado.
Se uma pessoa durante uma viagem, mantém pressionado o pedal do acelerador do carro em uma posição fixa, a aceleração produzida permanecerá constante. Dessa forma, a velocidade do veículo irá variar em taxas proporcionais durante o tempo do trajeto.
Dizemos então que a aceleração do objeto a é igual a sua aceleração média, ou seja:
Publicidade
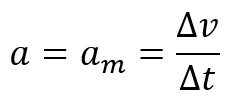
Esse tipo de movimento pode ocorrer em vários tipos de trajetórias, retas ou circulares. Especificamente quando a trajetória é uma reta, a movimentação do objeto é classificada como MRUV – movimento retilíneo uniformemente variado.
Além disso, podemos associar matematicamente as equações da velocidade e do espaço desse movimento. A equação da velocidade é apresentada como:
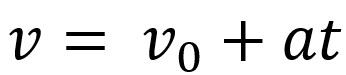
Na equação acima, temos que v é a velocidade final, v0 é a velocidade inicial, a é a aceleração e t o tempo em que o objeto realizou o movimento.
Temos também a equação do espaço para o MUV. Ela é utilizada para saber qual foi o espaço percorrido por um corpo durante um determinado intervalo de tempo. A equação é:
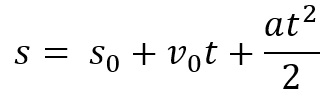
Neste caso, temos que s é o espaço total percorrido, s0 é o espaço inicial, ou seja, de onde o objeto saiu, v0 é a velocidade inicial, a é a aceleração e t o tempo do movimento.
Tipos de gráficos do MUV
O MUV pode ser expresso em três tipos de gráficos: aceleração por tempo, velocidade por tempo e espaço por tempo. Para o primeiro gráfico, temos a seguinte situação:
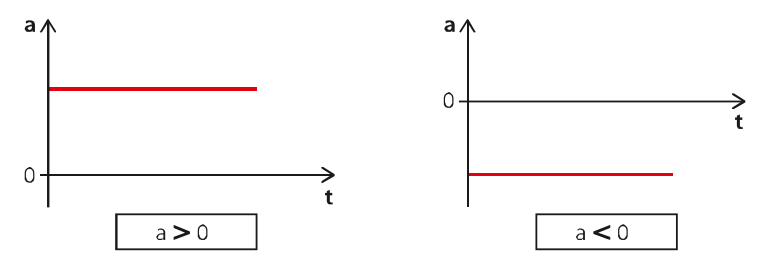
No gráfico à esquerda a aceleração é positiva e no da esquerda ela é negativa. Logo, no primeiro caso temos um movimento acelerado e no segundo, retardado.
Uma reta é o que representa o gráfico de velocidade por tempo, pois a equação da velocidade em função do tempo é uma equação do primeiro grau. Se a aceleração for positiva (a > 0), v(t) será uma função crescente:

Agora, se a aceleração for negativa (a < 0), então a função da velocidade será uma função decrescente:

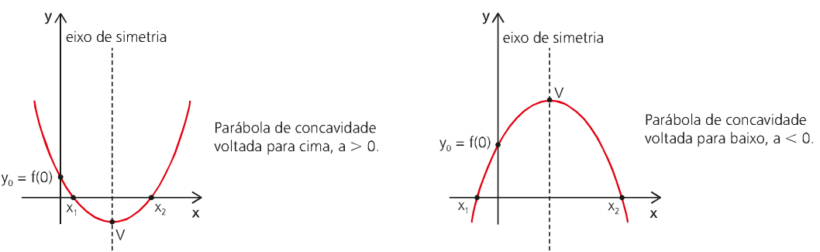
Como a função do espaço do MUV em função do tempo é uma função do segundo grau, o seu gráfico será representado por uma parábola.
Movimento uniforme x MUV
Como já foi visto, o movimento uniformemente variado é aquele que possui uma aceleração diferente de zero. A diferença para o movimento uniforme está justamente nesse ponto. No movimento uniforme, não existe aceleração e, portanto, o corpo mantém sua velocidade constante durante todo o trajeto.
MUV x movimento variado
Se um carro mantém a sua aceleração constante, então ele está em movimento uniformemente variado. Já o movimento variado é uma forma geral do primeiro caso, ou seja, a aceleração não é constante, porém a velocidade do objeto ainda varia durante um intervalo de tempo.
Videoaulas sobre movimento uniformemente variado
Para finalizar, confira vídeos que vão te auxiliar em um melhor entendimento do assunto:
Conceitos de MUV
Revise e entenda mais sobre os conceitos do MUV com este vídeo. Assim você garante que nenhuma dúvida vai ficar mal resolvida!
Equações e exemplos
Exemplos são sempre interessantes na hora de assimilar um conteúdo. Assista ao vídeo e fique craque nas equações e aplicações do MUV.
Exercício resolvido
Um exercício resolvido é importante para compreender como aplicar as equações desse conteúdo e fazer bonito na hora da prova.
E falando em prova, role a página para encontrar mais exercícios para testar seus conhecimentos e ficar ainda mais preparado!
Referências
Física para o ensino médio, vol. 1: mecânica – Kazuhito Yamamoto;
As faces da física – Wilson Carron.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Movimento uniformemente variado. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/movimento-uniformemente-variado. Acesso em: 02 de April de 2025.
1. [FUVEST]
Um veículo parte do repouso em movimento retilíneo e acelera com aceleração escalar constante e igual a 2,0 m/s2. Pode-se dizer que sua velocidade escalar e a distância percorrida após 3,0 segundos, valem, respectivamente:
a) 6,0 m/s e 9,0m;
b) 6,0m/s e 18m;
c) 3,0 m/s e 12m;
d) 12 m/s e 35m;
e) 2,0 m/s e 12 m.
Das informações do exercício, sabemos que
a = 2,0 m/s2
t = 3 s
v0 = 0 (pois o veículo parte do repouso)
Utilizamos então a equação v = v0 + at:
v = 0 + 2 . 3
v = 6 m/s
Também utilizamos a função horária do espaço para o movimento uniformemente variado:
S = S0 + v0t + (at²)/2
Como S0 e v0 são iguais a zero, reescrevemos a fórmula da seguinte forma:
S = (at²)/2
S = (2.3²)/2
S = 9 m
RESPOSTA: a)
2.
Um móvel parte do repouso e percorre uma distância de 200 m em 20 s. A aceleração desse móvel, em m/s², é:
a) 0,5
b) 0,75
c) 1
d) 1,5
e) 2
Os dados fornecidos pelo exercício são:
S = 200 m
t = 20 s
v0 = 0
Utilizamos, assim, a função horária da posição:
S = S0 + v0t + (at²)/2
200 = 0 + 0.20 + (a.20²)/2
200 = (a.400)/2
200 = 200.a
Isolando a aceleração
a = 200/200
a = 1 m/s²
RESPOSTA: c)