O MHS, ou Movimento Harmônico Simples, é um fenômeno físico que diz respeito às oscilações em um determinado intervalo de tempo. Ele acontece exclusivamente em sistemas conservativos. A descrição desse movimento é feita a partir da frequência e do período do movimento oscilatório. Veja o que é, suas características e muito mais.
Publicidade
O que é o MHS
O Movimento Harmônico Simples, ou MHS, é um movimento periódico. O qual acontece apenas em sistemas conservativos. Isto é, aqueles nos quais não há forças dissipativas. No caso do Movimento Harmônico Simples, as forças restauradoras atuam sempre para fazer o corpo voltar ao estado de equilíbrio.
Relacionadas
Nesse tipo de movimento oscilatório, existem algumas grandezas físicas envolvidas. Por exemplo, a frequência angular e o período. Os quais se relacionam por meio da quantidade de oscilações em um determinado intervalo de tempo. Já a amplitude é o tamanho da oscilação.
Características
Todo movimento tem suas características. Com o Movimento Harmônico Simples isso também acontece. Por isso, veja as cinco principais características desse tipo de movimento.
- O movimento é periódico e uniforme.
- A soma das energias cinéticas e potenciais são sempre constantes.
- Há a conservação da energia mecânica
- O MHS é definido a partir de grandezas angulares.
- O círculo trigonométrico é usado como referência para uma oscilação completa.
A partir dessas características é possível compreender e estudar as fórmulas para o Movimento Harmônico Simples. Veja quais são elas:
Fórmulas do MHS
As fórmulas do Movimento Harmônico Simples são obtidas as partir das frequências, do período e das funções horárias do movimento. Dessa forma, confira as relações matemáticas para esse tipo de movimento.
Publicidade
Equação da posição
Essa equação é usada para calcular a posição de um corpo que desenvolve um Movimento Harmônico Simples, após um determinado período de tempo. Matematicamente:
![]()
Em que:
Publicidade
- x: posição (m)
- t: tempo (s)
- A: amplitude (m)
- ω: frequência angular (rad/s)
- ϕ0: ângulo ou fase inicial (rad)
Nesse caso, o termo x(t) representa a posição do corpo após um determinado intervalo de tempo a partir do início do movimento.
Equação da velocidade
Quando se trata da velocidade no Movimento Harmônico Simples, ela depende da amplitude, a velocidade angular e do seno dos ângulos obtidos a partir do círculo trigonométrico. Matematicamente:
![]()
Em que:
- v: velocidade (m/s)
- t: tempo (s)
- A: amplitude (m)
- ω: frequência angular (rad/s)
- ϕ0: ângulo ou fase inicial (rad)
Note que a velocidade dependente do tempo, isto é, v(t), possui unidade de medida diferente da velocidade angular.
Equação da aceleração
A aceleração no Movimento Harmônico Simples é parecida com a equação da posição. Dessa forma, ela é definida como:
![]()
Em que:
- v: velocidade (m/s)
- t: tempo (s)
- A: amplitude (m)
- ω: frequência angular (rad/s)
- ϕ0: ângulo ou fase inicial (rad)
Nesse caso, o que se espera encontrar é a aceleração dependente do tempo. Isto é, a(t). Nessa equação não se calcula a aceleração angular.
Além das equações acima, existem relações matemáticas específicas para o cálculo de frequência, período e amplitude. Todas elas dependerão do tipo de sistema considerado. Por isso, elas podem exigir um formalismo matemático maior.
Vídeos sobre MHS
O Movimento Harmônico Simples é um conteúdo avançado e precisa ser estudado com calma. Por isso, aprofundar os conhecimentos sobre ele é importante para dominar todos os seus conceitos. Dessa forma, que tal assistir aos vídeos selecionados para aprender ainda mais?
Movimento Harmônico Simples
O professor Marcelo Boaro explica o que é o Movimento Harmônico Simples.Dessa maneira, ele relaciona tais conceitos com os conteúdos de ondulatória. Além disso, o professor explica as fórmulas desse fenômeno físico. Ao fim da videoaula, o professor Boaro resolve um exercício de aplicação.
Movimento Harmônico Simples e cinemática
Outra abordagem para o MHS é seu tratamento cinemático. Para compreender essa forma de estudar esse movimento, veja o vídeo do professor Douglas Gomes. Para isso, o docente relembra os conceitos de cinemática angular e como é possível estudá-los no círculo trigonométrico.
Conceitos iniciais do Movimento Harmônico Simples
Ao aprender um conteúdo novo, é preciso conhecer bem as suas bases. Por isso, o professor Davi Oliveira, do canal Física 2.0, explica os conceitos fundamentais do Movimento Harmônico Simples. Para isso, o docente relembra alguns conceitos de cinemática e ondulatória. Ao fim do vídeo, o professor Davi resolve um exercício de aplicação.
O estudo de conceitos das oscilações é importante para a compreensão do mundo externo. Essa área da Física pode dar início aos estudos de áreas mais avançadas da Física Moderna como é o caso da Física Quântica.
Referências
Física II: Oscilações e ondas (2016) – Hugh D. Young et al.
Física: Volume 2 (2008) – David Halliday et al.
Curso de Física Básica: Volume 2 (2014) – Herch Moysés Nussenzveig.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. MHS. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/mhs. Acesso em: 24 de April de 2025.
1. [Unitau]
Um corpo de massa m, ligado a uma mola de constante elástica k, está animado de um movimento harmônico simples. Nos pontos em que ocorre a inversão no sentido do movimento:
a) são nulas a velocidade e a aceleração
b) são nulas a velocidade e a energia potencial
c) o módulo da aceleração e a energia potencial são máximas
d) a energia cinética é máxima e a energia potencial é mínima
e) a velocidade, em módulo, e a energia potencial são máximas
Alternativa correta C.
Quando ocorre a inversão do sentido do movimento harmônico simples, a velocidade é nula e, consequentemente, a energia cinética também. Porém, a energia mecânica transforma-se completamente em energia potencial, que, por sua vez, assume seu máximo valor. Nesse instante, a aceleração também atinge seu valor máximo.
2. [UFG]
O gráfico mostra a posição, em função do tempo, de uma partícula em movimento harmônico simples no intervalo de tempo entre 0 e 4 segundos. A equação da posição em função do tempo para esse movimento é dada por x = a.cos(w.t + φ0). A partir do gráfico, encontre os valores das constantes a, w e φ0.
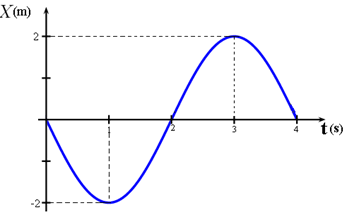
Analisando o gráfico percebemos que a posição do móvel que se encontra em mhs oscila entre os pontos 2 e -2. Logo, a amplitude do movimento equivale a 2m.
Velocidade angular w = 2.π.f
f = 1/T = 1/4 Hz
w = 2.(1/4).π
w = π/2 rad/s
A fase inicial é dada por
X = a.cos(wt + π}
X = 2.cos ([π/2].t + π
Analisando graficamente, temos que: T = 4s
w = 2. π.f = 2.π.1/4 = ½]