A Lei de Coulomb possibilita o cálculo da intensidade da força elétrica entre os corpos eletrizados. Foi determinada pelo físico francês Charles Augustin de Coulomb (1736-1806) a partir do experimento da balança de torção.
Publicidade
Coulomb constatou que corpos tinham uma interação diretamente proporcional ao produto entre os valores das cargas de cada corpo e inversamente proporcional ao quadrado da distância que os separavam.
Interações entre cargas
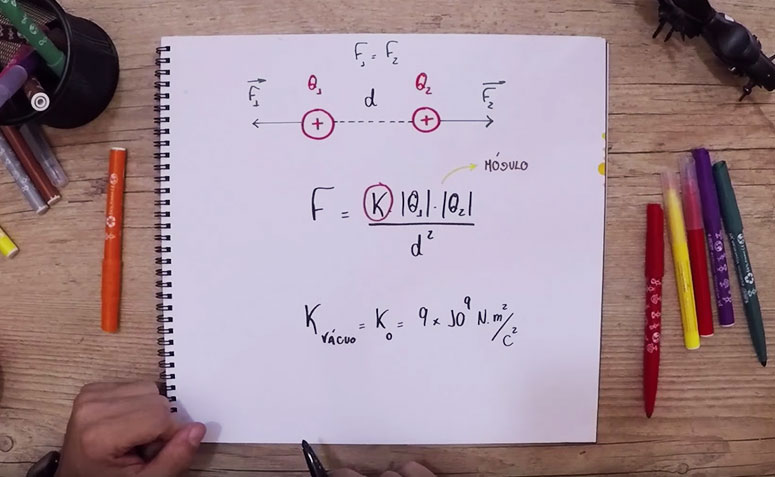
Antes de mais nada, vamos considerar dois corpos eletrizados, Q1 e Q2, separados por uma certa distância r. Ainda mais, como esses corpos são menores que a distância que os separam, logo podemos definir os corpos como pontos e chamá-los de cargas elétricas puntiformes. Dessa forma, um corpo puntiforme eletrizado é uma carga elétrica armazenada em um determinado ponto material.
Relacionadas
Nesta situação, onde os corpos estão eletrizados, existe uma interação elétrica entre eles, conhecida como força elétrica. Assim, podemos ter as seguintes interações:
- Se Q1 e Q2 estiverem eletrizados com cargas de mesmo sinal (positivo ou negativo), então a interação entre eles será de repulsão, sendo a força elétrica positiva. Em suma, os corpos vão se afastar um do outro;
- Se forem eletrizados com cargas de sinais contrários, a força elétrica será de atração e seu valor negativo. Em síntese, os corpos vão se aproximar.
Carga elétrica e seus submúltiplos
A princípio, um corpo puntiforme eletrizado possui uma certa quantidade de carga. A unidade da carga elétrica é definida pela unidade Coulomb (C).
Na eletrostática, quando uma partícula está eletrizada com carga Q = 1C, dizemos que ela está com uma carga muito alta. Portanto, é comum trabalhar com cargas menores que 1C. Então, utilizamos os submúltiplos, que são:
- milicoulomb: 1 mC = 10-3C;
- microcoulomb: 1 µC = 10-6C;
- nanocoulomb: 1 nC = 10-9C
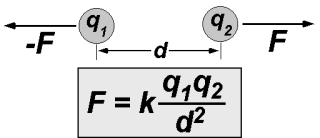
Fórmula da Lei de Coulomb
Publicidade
Observando a fórmula da lei de Coulomb, encontramos os seguintes itens:
- F = força elétrica entre as cargas (em newton – N);
- K = constante eletrostática no vácuo (ko = 9 x 109 N.m2/C2);
- q1 = corpo elétrico 1 eletrizado (em Coulomb – C)
- q2 = corpo elétrico 2 eletrizado (em Coulomb – C)
- d = distância que separam esses corpos (em metros – m)
Portanto, quando dois corpos eletrizados estiverem perto, uma força elétrica de atração ou repulsão irá surgir entre eles. Isso se deve ao fato de que a força elétrica é uma força de campo, assim como a força gravitacional.
Resumo
Enfim, podemos ver um resumo da lei de Coulomb a partir do vídeo a seguir:
Publicidade
Referências
As faces da Física – Wilson Carron e Osvaldo Guimarães
Física para o Ensino Médio: Eletricidade e Física Moderna – Kazuhito Yamamoto e Luiz Felipe Fuke

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Lei de Coulomb. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/lei-de-coulomb. Acesso em: 03 de April de 2025.
1. [UNIFESP-SP]
Duas partículas de cargas elétricas Q1 = 4,0 × 10-16C e Q2 = 6,0 × 10-16C estão separadas no vácuo por uma distância de 3,0.10-9m. Sendo k = 9,0.109 N.m2/C2, a intensidade da força de interação entre elas, em newtons, é de:
a) 1,2.10-5N.
b) 1,8.10-4N.
c) 2,0.10-4N.
d) 2,4.10-4N.
e) 3,0.10-3N.
Sabemos que a lei de Coulomb é:
F = (k . Q1 . Q2)/d2
substituindo os respectivos valores de k, Q1, q e d na lei de Coulomb, temos
F = (9,0×109 . 4,0 × 10-16 . 6,0 × 10-16)/(3,0×10-9)2
No numerador vamos multiplicar 9 por 6 e no denominador multiplicamos 3 por 3. As potências de base 10 no numerador mantemos como está e no denominador repetimos a base e somamos os expoentes. Com isso, temos que
F = (3,0×109 . 4,0 × 10-16 . 2,0 × 10-16)/(10-18 )
Multiplicando agora 2, 3 e 4 no numerador entre eles, repetindo os expoentes de base 10 e mantendo a potência de base 10 no denominador, obtemos
F = (24×109× 10-16× 10-16)/(10-18 )
Repetindo agora as potências de base 10 no numerador e somando seus expoentes, obtemos
F = (24×10-23)/(10-18 )
“Passando” a potência de base 10 do denominador para o numerador com o expoente positivo e somando os expoentes, temos
F = 24×10-5
Andando uma casa com a vírgula para a esquerda, obtemos a resposta
F = 2,4×10-4 N
Resposta: d
2. [UF JUIZ DE FORA]
Duas esferas igualmente carregadas, no vácuo, repelem-se mutuamente quando separadas a uma certa distância. Triplicando a distância entre as esferas, a força de repulsão entre elas torna-se:
a) 3 vezes menor
b) 6 vezes menor
c) 9 vezes menor
d) 12 vezes menor
e) 9 vezes maior
Inicialmente, temos a seguinte força de atração entre as esferas
F = (k . Q1 . Q2)/d2
Quando triplicamos a distância entre elas, temos que d = 3d’, logo a nova força de atração será
F’ = (k . Q1 . Q2)/(3d’)2
F’ = (k . Q1 . Q2)/9d’2
Como F = (k . Q1 . Q2)/d2 então a nova força será
F’ = F/9
ou seja, será nove vezes menor.
Resposta: c