Quando aplicamos uma determinada força para mover algum objeto em um curto período de tempo, essa força realiza o que chamamos de impulso. Em outras palavras, o impulso é a ação de uma determinada força durante um certo intervalo de tempo.
Publicidade

O impulso dependerá, então, da força aplicada e do tempo que essa força for aplicada, ou seja, quanto maior a força maior será o impulso. O mesmo serve para o tempo. Quanto maior o tempo, maior o impulso aplicado a um certo objeto. A unidade de medida do impulso no Sistema Internacional de medidas é o N∙s (Newton∙segundo) .
Fórmula do impulso
Assim como em muitas áreas da física, o impulso pode ser expresso através de uma fórmula geral. Ela pode ser observada a seguir:
Relacionadas
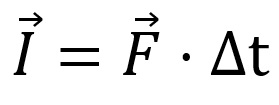
Sabemos que uma força é uma grandeza vetorial. Porém, o tempo é uma grandeza escalar e quando multiplicamos uma grandeza vetorial por um escalar, o resultado obtido é uma grandeza vetorial. Dessa forma, o impulso também é uma grandeza vetorial, ou seja, precisa de um sentido, direção e módulo (tamanho) para ser bem definido.
Para conseguirmos calcular o impulso precisamos saber qual a força que foi aplicada sobre um objeto qualquer e qual foi o tempo que essa força foi aplicada.
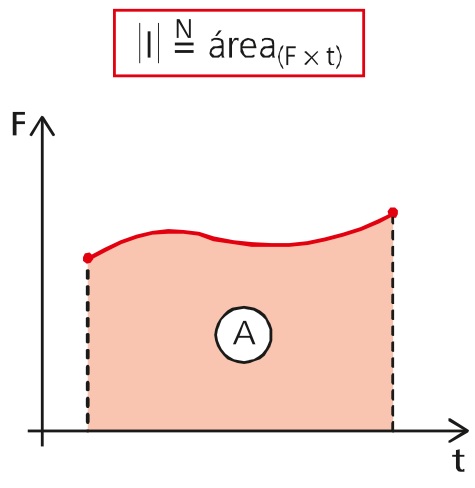
Gráfico do impulso
Publicidade
Em um gráfico de Força por tempo, como o da figura acima, podemos obter o impulso aplicado em um determinado objeto apenas calculando a área abaixo do gráfico.
Quantidade de movimento
Uma carreta carregada demora muito mais para atingir uma certa velocidade quando comparada a um carro mais leve. O mesmo serve para a freagem da carreta, ou seja, ela demora muito mais para frear do que o carro, tendo ambos a mesma velocidade. A isso, damos o nome de quantidade de movimento. No nosso exemplo a carreta possui uma quantidade de movimento maior que a do carro.
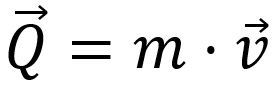
Publicidade
Quantidade de movimento é definido pela multiplicação da massa de um objeto pela sua velocidade, como podemos ver na fórmula acima. Além disso, a quantidade de movimento também é uma grandeza vetorial, em outras palavras, ela precisa de um sentido, direção e módulo para ser bem definida. Sua unidade no S.I é o Kg⋅m/s.
Teorema do impulso
O teorema do impulso nos diz que:
O impulso resultante de um sistema de forças sobre um corpo é igual a variação da quantidade de movimento do corpo.
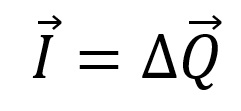
Em outras palavras, quando uma força resultante age sobre um corpo ela varia a sua velocidade, logo a quantidade de movimento também varia. Mas quando essa força é aplicada em um certo intervalo de tempo, então teremos que o impulso é igual a variação da quantidade de movimento.
Exemplos de impulso
No nosso cotidiano podemos aplicar o impulso em muitas situações. Vamos então entender em quais ocasiões o impulso ocorre.
- Para-choques de carros: os para-choques são feitos, atualmente, de materiais elásticos. Dessa forma, o tempo de contato entre o para-choque e o local da colisão é maior, diminuindo assim a força resultante que agirá no carro. Com isso, os passageiros no interior do carro sofrem menos com o impacto;
- Boxeador: quando um boxeador erra o tempo da defesa de um golpe, ele realiza um movimento com a cabeça para trás de tal forma que o tempo de impacto do soco aumente, diminuindo então a força resultante da pancada;
- Pulando de uma altura qualquer: ao pularmos de uma certa altura mantemos nossas pernas esticadas durante a queda e depois dobramos os joelhos quando tocamos o chão. Isso ajuda a aumentar o tempo de contato com o chão e, assim, diminuir a força resultante de impacto com o chão.
Existem muitos outros exemplos de impulso que podemos aplicar no nosso dia a dia. Os foguetes que vão para o espaço também são um grande exemplo de impulso.
Videoaulas sobre impulso
Tendo o conceito de impulso e quantidade de movimento em mente, vamos, dessa forma, nos aprofundar mais no assunto a partir dos vídeos a seguir.
Definição e exercícios resolvidos sobre impulso
O primeiro vídeo abordará a definição de impulso e quantidade de movimento. Além disso, o vídeo apresenta alguns exercícios resolvidos sobre o assunto.
Uma breve explicação do teorema do impulso e um exemplo
Por outro lado, o segundo vídeo nos apresenta uma breve explicação do teorema do impulso e no fim apresenta um exemplo da aplicação desse teorema.
A definição de quantidade de movimento
No terceiro vídeo, podemos entender um pouco melhor a quantidade de movimento além de observarmos um exemplo sobre esse tema.
Por fim, o teorema do impulso é muito importante para o nosso dia a dia. Quando entendemos o conceito, conseguimos então entender o fato pelo qual nós conseguimos chutar uma bola, lançar dardos, nos proteger de acidentes de carro entre muitas outras aplicações do impulso.
Referências
Física para o ensino médio, vol. 1 : mecânica – Kazuhito Yamamoto;
As faces da física – Wilson Carron.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Impulso. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/impulso. Acesso em: 03 de April de 2025.
1. [PUC – MG]
Uma força de 6 N atuando sobre um objeto em movimento altera sua quantidade de movimento em 3kg . m/s. Durante quanto tempo essa força atuou sobre esse objeto?
a) 1s
b) 2s
c) 0,25
d) 0,50
Dados
F = 6 N
ΔQ = 3Kg . m/s
Utilizamos a equação do teorema do impulso e quantidade de movimento:
ΔQ = I
ΔQ = F.t
3 = 6 . t
3 = t
6
t = 0,50 s
Resposta: d)
2.
O gráfico a seguir representa a variação da intensidade da força F em função do tempo:
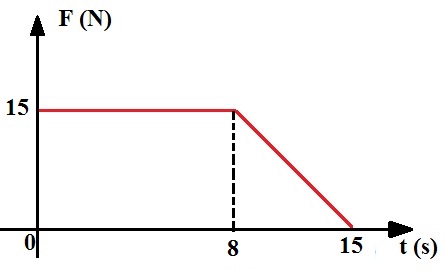
Calcule o impulso da força no intervalo de 15s.
O impulso da força F é igual à área sob a curva do gráfico da força x tempo.
A área desse gráfico é igual à soma da área do retângulo, de 0 a 8 s, com a área do triângulo no intervalo de 8 a 15 s.
A área do retângulo é calculada pelo produto entre a sua base e altura:
Ar = b x h
Ar = 8 . 15
Ar = 120
A área do triângulo é dada pelo produto entre a base e a altura dividido por 2:
At = (b x h)/2
At = (7 x 15)/2
At = 105/2
At = 52,5
I = Atotal
I = Ar + At
I = 120 + 52,5
I = 172,5 N.s