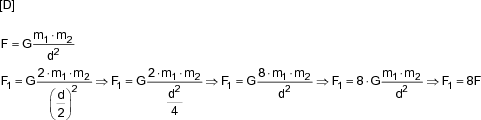Gravitação Universal

A lei da gravitação universal afirma que dois corpos que possuem massa estão sujeitos a uma atração mútua. Esta atração é diretamente proporcional ao produto das massas e ao inverso do quadrado da distância que os une. A teoria da gravitação foi elaborada por Isaac Newton com base em outros estudos de sua época, como os postulados de Johannes Kepler.

Publicidade

O que é a gravitação universal?

Um dos primeiros questionamentos nos campos das Ciências estavam relacionados ao que as pessoas viam durante a noite. Por exemplo, por que a Lua não cai do céu? Estamos no centro do universo? Como os planetas se movimentam? Com o desenvolvimento das teorias da gravitação as respostas para estas perguntas começaram a ficar mais claras e cada vez dependiam menos de explicações místicas.

Durante o desenvolvimento humano, surgiram diversas respostas às perguntas sobre nossa posição e interação com o universos. Algumas delas se destacaram. Porém, devemos considerá-las dentro de suas limitações teóricas, observacionais e de contexto histórico e social. Desta forma, não devemos enxergar as teorias antigas como erradas ou menos científicas.

Nicolau Copérnico e o sistema heliocêntrico

Uma das teorias que merecem ser destacadas é a concepção de Nicolau Copérnico (1473-1543) sobre o movimento planetário. Este astrônomo propôs uma ideia de um sistema planetário no qual o Sol estava no centro em vez da Terra, como era aceito naquela época. Essa ideia já havia sido proposta pelos gregos, porém foi abandonada. Atualmente, esse episódio é chamado de Revolução Copernicana, devido a sua importância para Ciência.

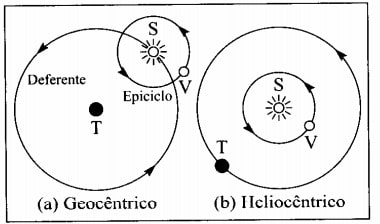
O que Copérnico espera mostrar com seu sistema planetário é que ele era muito mais simples de se explicar que o sistema Geocêntrico (com a Terra no centro). Com o sistema copernicano, era possível explicar todos os fenômenos explicados pelo sistema antigo. Por exemplo, para o movimento do planeta Vênus, o sistema geocêntrico aceito até então assumia que a Terra estava no centro com o sol girando em torno dela e Vênus girando em torno do Sol. Já o sistema copernicano (heliocêntrico) está mais próximo do que conhecemos atualmente, como o Sol no centro e os planetas girando em torno dele.

Publicidade

Johannes Kepler e as órbitas dos planetas

Por conta das teorias de Copérnico, a astronomia observacional daquela época ganhou um novo fôlego. No século XVI, o dinamarquês Tycho Brahe (1546-1601) fez observações das estrelas muito importantes para a astronomia. Entretanto, Brahe não era defensor das ideias copernicanas. Então, propôs um modelo intermediário entre o heliocêntrico e o geocêntrico.

Publicidade

Com a morte de Brahe, seus dados observacionais ficaram com seu assistente e sucessor Johannes Kepler (1571-1630). Contudo, diferente de seu tutor, Kepler acreditava que o universo pudesse ser explicado a partir de argumentos de perfeição e da harmonia dos planetas. Com isso, ele foi capaz de postular três leis para o movimento planetário:

Johannes Kepler

Primeira Lei de Kepler (lei das órbitas)

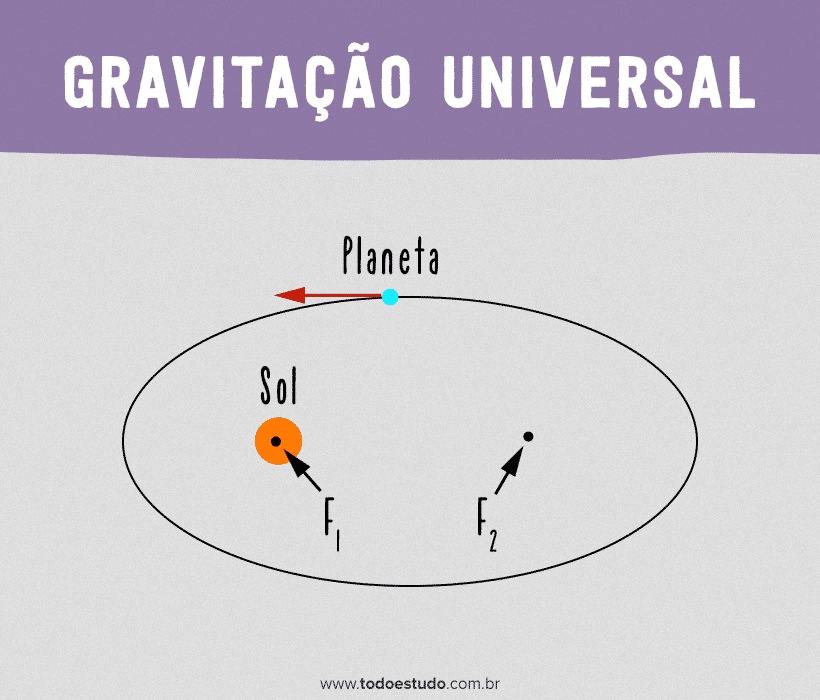
Para que seus modelos pudessem ser válidos, Kepler supôs que o Sol não ocupava exatamente o centro da órbita. Ele propôs que a órbita de um planeta fosse elíptica e o Sol estaria em um dos focos da elipse.

Segunda Lei de Kepler (lei das áreas)

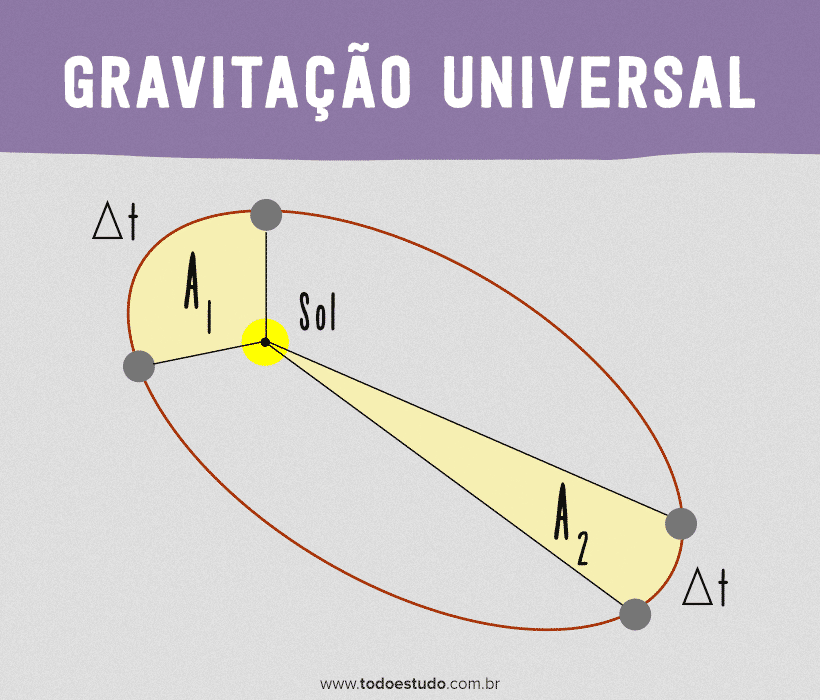
No momento em que o planeta está mais próximo do sol, ele percorre uma distância maior do que a distância percorrida no mesmo intervalo de tempo quando ele está mais longe do Sol. Entretanto, se considerarmos as áreas delimitadas pelo segmento de reta que liga o planeta ao Sol, elas serão iguais. Ou seja, um planeta descreve áreas iguais em tempos iguais.

Terceira Lei de Kepler (lei dos períodos)

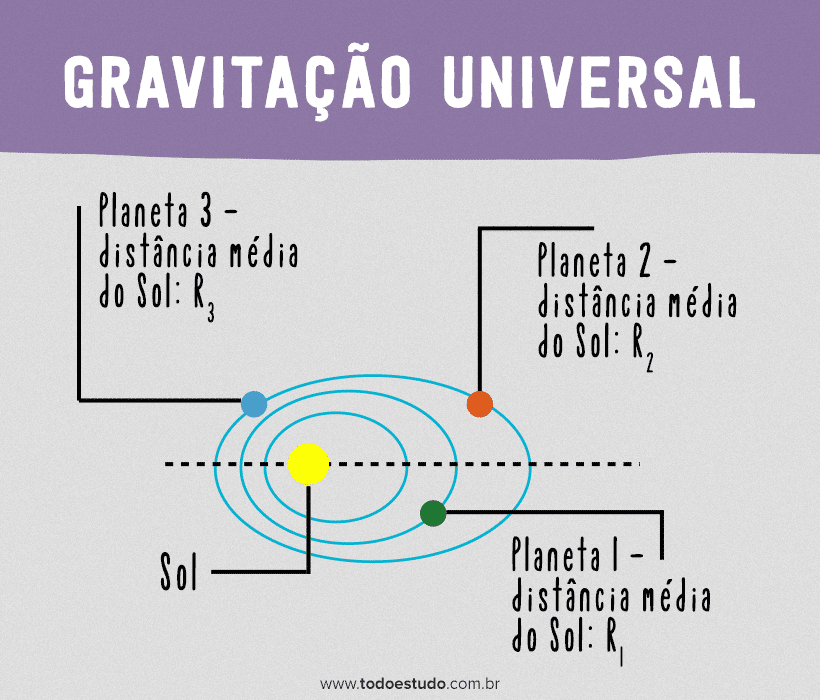
Considerando dois planetas diferentes com períodos T e raios médios R distintos, há uma relação de proporção que é a terceira lei de Kepler. O quociente entre o quadrado dos períodos e o cubo dos raios médios é igual a uma constante para todos os planetas. Matematicamente:

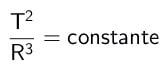
Em que,

• T: período de rotação do planeta (unidade de medida de tempo);
• R: raio médio da órbita (unidade de medida de distância).

Isaac Newton e a gravitação universal

Há uma lenda científica que diz que Isaac Newton descobriu a lei da gravitação universal quando uma maçã caiu em sua cabeça. Contudo, essa história é falsa em vários níveis. O que realmente ocorreu foi que Newton – baseado em estudos anteriores (como o de Kepler, Galileu Galilei e outros) – conseguiu postular uma lei de interação da distância entre dois corpos com massa. Newton publicou essa lei juntamente com as suas três leis do movimento.

É interessante notar que Newton assumia que a interação entre os corpos era dada à distância, sem campos gravitacionais. Ou seja, ele não aceitava que um ente puramente matemático (como os campos gravitacionais) pudessem interagir com a matéria.

Com base na lei da gravitação universal de Newton, é possível, por exemplo, colocar satélites em órbita ou realizar viagens espaciais. Além disso, a lei da gravitação é fundamental para entender o movimento das marés,

Fórmula da gravitação universal

Os efeitos mais evidentes da lei da gravitação universal de Newton só são observáveis em escalas astronômicas. A lei da gravitação universal nos diz que:

Cada partícula do universo atrai qualquer outra partícula com uma força diretamente proporcional ao produto das massas e inversamente proporcional ao quadrado da distância entre as partículas.

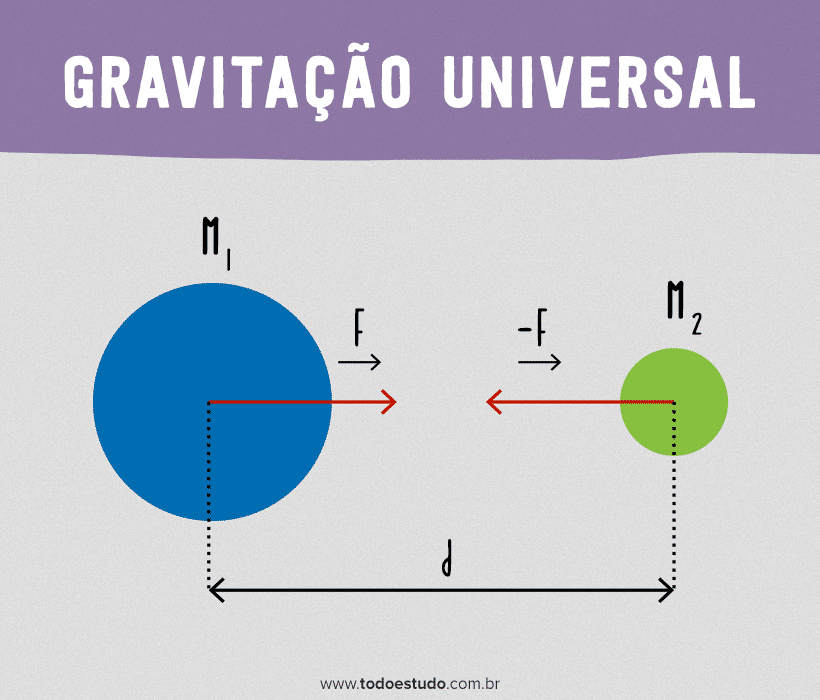
Matematicamente:

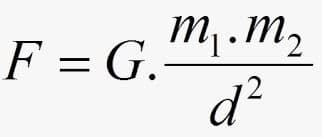
Em que,

• F: força de atração gravitacional (N)
• m₁: massa do corpo 1 (kg);
• m₂: massa do corpo 2 (kg);
• d: distância entre os dois corpos (m);
• G: constante da gravitação universal (N m²/kg²).

Com esta fórmula, é possível ver que a força entre dois corpos diminui conforme o aumento da distância entre eles. Por exemplo, se a distância dobrar, a força se reduzirá a um quarto da força original. Além disso, é importante notar que a força gravitacional (assim como outras forças que atuam a distância) está ao longo da linha reta que une os dois corpos.

Constante de gravitação universal

A constante G, chamada de constante da gravitação universal, é uma constante de proporcionalidade característica da força gravitacional. Seu valor pode variar conforme o sistema de unidades adotado.

Assumindo unidades do Sistema Internacional de Unidades (SI), o valor numérico aproximado da constante da gravitação universal é:

G = 6,67 x 10 ^-11 N m²/kg²

Vídeos sobre a gravitação universal

Agora que já estudamos e entendemos a aplicação da gravitação universal em nosso dia a dia, vamos aprofundar nossos conhecimentos.

Força gravitacional

Neste vídeo, você se aprofundará em seus conhecimentos conceituais e matemáticos sobre a lei da gravitação universal

Gravitação de Newton

Aqui, você verá de maneira avançada os conceitos da gravitação newtoniana.

A física dos satélites

Veja uma aplicação direta da lei da gravitação de Newton ao estudar a física por trás dos satélites.

Como vimos a gravitação universal permeia o pensamento da humanidade desde a antiguidade. Além disso, com os avanços do entendimento sobre a gravitação, foi possível descrever melhor o mundo a nossa volta, bem como enviar o ser humano ao espaço e explorar outros planetas. Parte do progresso, deve-se a teoria elaborada por Isaac Newton.

Referências