No nosso dia a dia encontramos vários equipamentos que nos auxiliam como as geladeiras e os carros. Algo em comum entre eles é um motor térmico que gera energia e força para o funcionamento dessas máquinas, em que a maior parte dessa energia é desperdiçada. Mas existe uma teoria, o ciclo de Carnot, que pode explicar melhor esse problema.
Publicidade
A teoria foi descoberta por Nicolas Léonard Sadi Carnot (1796-1832), que diz a respeito de uma máquina térmica que realiza um ciclo de rendimento teórico máximo. Dessa forma, estudaremos a seguir sobre esse ciclo, o seu diagrama de etapas termodinâmicas, o teorema, a equação do rendimento e o que seria uma máquina térmica ideal.
Relacionadas
Diagrama e etapas do Ciclo de Carnot
Quando uma determinada massa de gás sofre várias transformações e retorna ao seu estado inicial de pressão, temperatura e volume chamamos essa transformação de cíclica. Uma máquina térmica, em geral, é uma combinação de ciclos termodinâmicos e cada um com seu determinado rendimento.
Sadi Carnot então conseguiu propor um ciclo termodinâmico que possui um rendimento teórico máximo. Independentemente da substância gasosa, esse rendimento ocorre em 4 processos termodinâmicos reversíveis: dois isotérmicos e dois adiabáticos. Esse ciclo pode ser observado no diagrama a seguir.
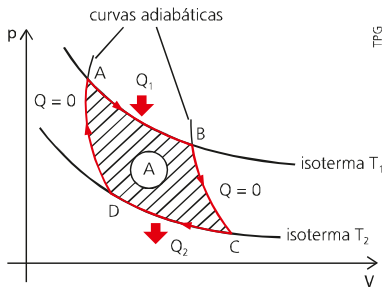
Vamos então entender um pouco sobre esse diagrama.
Publicidade
- Primeira etapa: o gás sofre uma transformação isotérmica (temperatura constante) AB, onde a máquina térmica adquire uma quantidade Q1 da fonte quente sob a temperatura T1;
- Segunda etapa: ocorre uma expansão adiabática BC, ou seja, não existe troca de calor (Q=0), mas uma diminuição de temperatura de T1 para T2;
- Terceira etapa: aqui ocorre uma compressão térmica CD. Em outras palavras, a máquina descarta uma quantidade de calor Q2 para a fonte fria de temperatura T2 (menor que T1);
- Quarta etapa (finalização do ciclo): compressão adiabática DA. Ocorre sem troca de calor (Q=0), mas existe um aumento de temperatura de T2 para T1.
Nos processos adiabáticos a entropia do sistema se mantém constante, pois não existe troca de calor com o meio.
Teorema de Carnot
A partir do diagrama anterior, Carnot conseguiu deduzir um teorema que leva o seu nome. O teorema é apresentado a seguir:
“Nenhuma máquina térmica que opere entre duas dadas fontes, às temperaturas T1 e T2, podem ter maior rendimento que uma máquina de Carnot operando entre estas mesmas fontes.”
Publicidade
Além disso, todas as máquinas de Carnot apresentam o mesmo rendimento se estiverem operando nas mesmas temperaturas T1 e T2. Esse teorema pode ser representado por uma equação matemática que é apresentada logo abaixo.
Fórmula
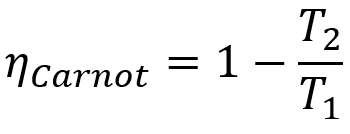
- ηCarnot: rendimento de uma máquina de Carnot;
- T1: temperatura da fonte quente;
- T2: temperatura da fonte fria.
A máquina térmica ideal
Uma máquina térmica é considerada ideal se seu rendimento for de 100%. Em outras palavras, toda a energia fornecida a essa máquina seria integralmente convertida em trabalho. Porém, isso é impossível de se acontecer, devido ao rendimento de Carnot.
Para que uma máquina térmica seja considerada ideal, a fonte fria deve estar a zero Kelvin (0K). Mas na natureza isso é impossível. Dessa forma, uma máquina ideal não existe.
Um pouco mais sobre ciclo de Carnot
Para você fixar melhor esse conteúdo e se dar bem nas provas, apresentamos a seguir alguns vídeos sobre o ciclo de Carnot.
Nome do assunto tratado no vídeo
Aqui você tira todas as dúvidas sobre o clico de Carnot que possam ter ficado para trás.
Exemplo de aplicação da equação de rendimento
Para que você entenda como aplicar a equação de rendimento de uma máquina de Carnot, apresentamos esse vídeo com um exemplo dessa aplicação!
Outra aplicação da equação de rendimento
Para que você se saia muito bem nas provas, apresentamos mais um exemplo resolvido sobre o rendimento de uma máquina de Carnot e sua equação!
Por fim, seria interessante a revisão do conteúdo de termodinâmica. Bons estudos!
Referências
As faces da física – Wilson Carron e Osvaldo Guimarães;
Física para o ensino médio, volume 2 – Kazuhito Yamamoto e Luiz Felipe Fuke.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Ciclo de Carnot. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/ciclo-de-carnot. Acesso em: 30 de March de 2025.
1.
Uma máquina térmica de Carnot tem sua fonte quente a uma temperatura de 227 ºC, enquanto a sua fonte fria opera a 27 ºC. O rendimento dessa máquina é igual a:
a) 16%
b) 88%
c) 40%
d) 25%
e) 50%
Podemos utilizar a equação do rendimento de uma máquina de Carnot
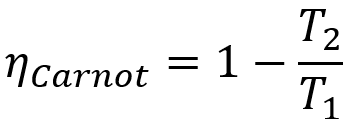
As temperaturas devem estar na escala Kelvin. A temperatura mais alta é a da fonte quente e a mais baixa é a da fonte fria. Vamos então converter essas temperaturas para a escala Kelvin
T1 = 227 + 273 = 500K
T2 = 27 + 273 = 300K
Assim, substituindo esses valores na equação de rendimento, obtemos
ηCarnot = 1 – (300/500)
ηCarnot = 1 – 0,6
ηCarnot = 0,4
Em porcentagem esse valor é 40%.
RESPOSTA: b)
2.
Julgue os itens a seguir como verdadeiros (V) ou falsos (F):
I – A máquina de Carnot é a única que pode assumir rendimentos de até 100%;
II – O Ciclo de Carnot é caracterizado por quatro transformações termodinâmicas reversíveis;
III – Nenhuma máquina que opere entre duas temperaturas fixadas pode ter rendimento maior que a máquina ideal de Carnot atuando nessas mesmas temperaturas.
São(é) verdadeira(s):
a) I
b) II
c) I e II
d) II e III
e) I, II e III
I – Falsa. Mesmo tendo a máquina de Carnot, que possui o maior rendimento possível para uma máquina térmica, é impossível alcançar um rendimento de 100%, já que isso violaria a Terceira Lei da Termodinâmica.
II – Verdadeira. O ciclo de Carnot é definido por quatro etapas: duas contrações, sendo uma adiabática e uma isotérmica, e duas expansões, uma também adiabática e outra isotérmica.
III – Verdadeira. A afirmação é o próprio postulado de Carnot.