Fórmulas de Física

As fórmulas de Física são importantes para o estudo quantitativo de determinados fenômenos naturais. Além disso, estudar essas relações matemáticas faz com que seja possível relacionar as grandezas físicas com o que é observado. Dessa forma, veja as fórmulas de 10 temáticas importantes da Física. Confira e prepare-se para as provas do Enem, vestibulares e concursos!

Publicidade

Cinemática

A cinemática é a área da Física que estuda o movimento. Contudo, esse campo de estudo não se preocupa com as causas dos movimentos. Dessa forma, suas fórmulas descrevem apenas o que acontece durante o movimento. De maneira geral, elas relacionam as posições, velocidades e acelerações.

Velocidade Média

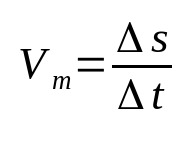
Em que:

• Δs: deslocamento (m)
• Δt: intervalo de tempo (s)
• V_m: velocidade média (m/s)

A velocidade média relaciona o deslocamento com o tempo percorrido. Ou seja, ela significa que um determinado objeto muda sua posição na taxa de variação encontrada. Por exemplo, afirmar que um corpo tem velocidade média de 12 m/s significa que, a cada segundo, ele se deslocou 12 metros. Essa é uma das mais básicas fórmulas de Física.

Aceleração média

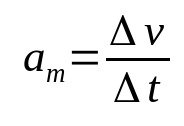
Publicidade

Em que:

• Δv: variação da velocidade (m/s)
• Δt: intervalo de tempo (s)
• a_m: aceleração média (m/s²)

A aceleração de um corpo é a taxa com a qual a velocidade varia no tempo. Dessa forma, a sua unidade de medida é o metro por segundo ao quadrado (m/s²). Isto é, para um corpo com aceleração média de 10 m/s², sua velocidade deve variar 10 m/s a cada segundo.

Função horária dos espaços

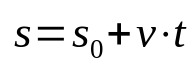
Publicidade

Em que:

• s: posição final (m)
• s₀: posição inicial (m)
• v: velocidade (m/s)
• t: tempo (s)

Note não haver aceleração na equação acima. Isso acontece porque ela descreve um movimento retilíneo uniforme. Além disso, essa função horária relaciona a posição após um determinado móvel se movimentar durante um certo tempo. Ou seja, para cada momento escolhido, a posição do móvel será diferente. Dessa forma, ela é uma relação matemática que possui a dependência no tempo.

Função horária da velocidade

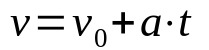
Em que:

• v: velocidade final (m/s)
• v₀: velocidade inicial (m/s)
• a: aceleração (m/s²)
• t: tempo (s)

Quando o movimento é retilíneo e uniformemente variado (MRUV), deve-se considerar a aceleração do corpo, que é constante. Além disso, essa função horária auxilia na determinação da velocidade de um móvel após um tempo t cuja aceleração é constante.

Função horária dos espaços no MRUV

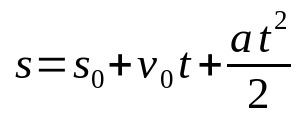
Em que:

• s: posição final (m)
• s₀: posição inicial (m)
• v₀: velocidade inicial (m/s)
• a: aceleração (m/s²)
• t: tempo (s)

Equação de Torricelli

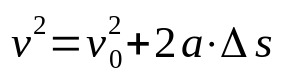
Em que:

• v: velocidade final (m/s)
• v₀: velocidade inicial (m/s)
• a: aceleração (m/s²)
• Δs: deslocamento (m)

A equação de Torricelli não depende do tempo. Ou seja, ela é uma relação da velocidade que depende do espaço. Por conta disso, ela é usada para determinar a velocidade de um móvel que desenvolve um movimento retilíneo uniformemente variado, sem ser necessário conhecer o tempo decorrido no deslocamento.

A partir dessas fórmulas de cinemática, é possível encontrar as demais relações dessa área da Física. Por exemplo, as equações dos movimentos verticais são derivadas das funções horárias citadas acima. Além disso, as relações para os movimentos circular também podem ser encontradas a partir das fórmulas supracitadas.

Mecânica

A Mecânica, também conhecida como Dinâmica, é a área da Física que estuda as causas dos movimentos. Por conta disso, suas fórmulas relacionam massa e aceleração. As leis de Newton fazem parte dos estudos da Mecânica. Porém, apenas duas delas podem ser descritas matematicamente.

Segunda lei de Newton

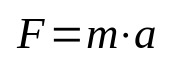
Em que:

• F: força (N)
• m: massa (kg)
• a: aceleração (m/s²)

Essa equação também é chamada princípio fundamental da dinâmica, sendo uma das mais importantes fórmulas de Física. Ela significa que o ato de tirar um objeto da inércia requer a aplicação de uma aceleração sobre ele. No sistema internacional de unidades (SI), a unidade de medida de força é dada em newtons, que é igual a quilograma vezes metro por segundo ao quadrado (kg m/s²).

Terceira lei de Newton

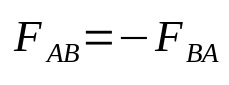
Em que:

• F_AB: força que o corpo A faz no corpo B (N)
• F_BA: força que o corpo B faz no corpo A (N)

A terceira lei de Newton afirma que toda ação tem uma reação de mesma intensidade e sentido oposto, ao longo da linha reta que une os dois corpos. Contudo, em certos casos, há a quebra nessa simetria. Assim, os corpos interagentes não obedecem a esse princípio da natureza. Por exemplo, quando se estuda a interação entre elementos infinitesimais de corrente. A teoria atualmente aceita pelos cientistas salva as aparências inserindo um conceito físico para correção desse erro conceitual.

Força peso

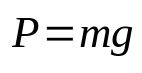
Em que:

• P: força peso (N)
• m: massa (kg)
• g: aceleração da gravidade no local (m/s²)

Ao contrário do que o senso comum afirma, peso e massa são conceitos distintos. O peso do corpo muda conforme a aceleração da gravidade no local. Dessa forma, essa força está relacionada com a atração gravitacional exercida sobre o corpo. Por sua vez, a massa é a medida da quantidade de matéria que um determinado objeto possui.

As principais fórmulas da mecânica permitem chegar às outras relações conhecidas. Cada uma delas dependerá do contexto a ser analisado. Por exemplo, em um plano inclinado, a componente da força peso sobre um corpo depende do ângulo de inclinação. Além disso, na teoria newtoniana, a soma das forças sobre um corpo deve ser igual ao produto da sua massa e aceleração.

Gravitação

Quando corpos celestes interagem entre si, há uma força de interação. Essa relação é dada pela Lei da Gravitação de Newton. Ela foi proposta considerando a interação pura entre matéria, sem levar em consideração campos puramente matemáticos interagindo com a matéria física. Além disso, na gravitação também existem as leis de Kepler, que descrevem o movimento planetário. Confira:

Lei da gravitação de Newton

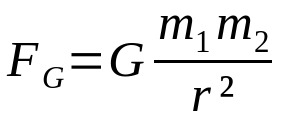
Em que:

• F_G: força gravitacional (N)
• G: constante da gravitação universal (6,67 x 10^-11 Nm²/kg²)
• m₁: massa do corpo 1 (kg)
• m₂: massa do corpo 2 (kg)
• r: distância entre os centros de massa dos dois corpos interagentes (m)

Essa lei foi desenvolvida considerando apenas a interação a distância entre os corpos. Além disso, assim como a Lei de Coulomb e a Força entre elementos de corrente de Ampère, essa relação depende do inverso do quadrado da distância. Ou seja, a força entre os corpos que interagem cai com o quadrado da distância entre eles. As relações que dependem do inverso do quadrado são fórmulas de Física muito comuns.

Terceira lei de Kepler

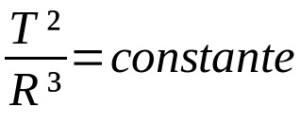
Em que:

• T: período orbital (unidade de tempo)
• R: raio médio da órbita (unidade de distância)

As demais leis de Kepler para o movimento planetário são qualitativas. Isto é, elas são uma descrição dos movimentos. Dessa forma, elas não dependem necessariamente de descrições matemáticas. A terceira lei de Kepler, por sua vez, descreve uma relação de proporção entre os períodos de órbita e o raio médio de uma órbita planetária. Nesse caso, as unidades de medida variam conforme a situação considerada.

Os estudos da gravitação intrigam o ser humano há milhares de anos. Desde a antiguidade, civilizações muito avançadas, como os povos asiáticos e os pré-colombianos, estudaram o movimento planetário. Atualmente, estuda-se baseado nas teorias atualmente aceitas pela comunidade científica.

Trabalho e energia

Ao colocar um corpo em movimento, há a conversão de energia – que, nesse caso, é a energia mecânica. Além disso, o movimento de um corpo também realiza trabalho. Essas grandezas físicas estão relacionadas e, além da mecânica, trabalho e energia podem se relacionar em outras áreas da Física.

Trabalho

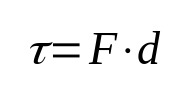
Em que:

• τ: trabalho (J)
• F: força (N)
• d: deslocamento (m)

O trabalho na Física, por definição, relaciona a força aplicada sobre um corpo e seu deslocamento. Ou seja, quando um corpo se desloca devido à ação de uma força, há a realização de trabalho. Sua unidade de medida no Sistema Internacional de Unidades é o joule.

Energia cinética

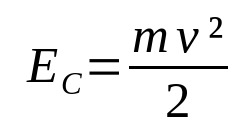
Em que:

• E_C: energia cinética (J)
• v: velocidade (m/s)
• m: massa (kg)

Quando um determinado corpo está em movimento, há uma energia associada a ele. Essa é a energia cinética. Isto é, a energia do movimento. Ela depende da massa do corpo e sua velocidade. Note que a energia cinética e a velocidade são diretamente proporcionais. Quanto maior for a velocidade, maior será a energia cinética, desde que a massa se mantenha constante.

Energia potencial

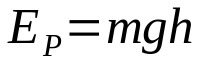
Em que:

• E_P: energia cinética (J)
• m: massa (kg)
• g: aceleração da gravidade no local (m/s²)
• h: altura em relação ao solo (m)

Se um corpo encontra-se a uma determinada altura do solo, ele possui uma energia potencial. Ou seja, ele tem a possibilidade de entrar em movimento. A energia potencial e a altura são diretamente proporcionais. Isso significa que, quanto maior for a altura em relação ao solo, maior será a energia potencial.

As relações de trabalho e energia servem tanto para o movimento dos corpos quanto para outras áreas da Física. Por exemplo, para termodinâmica. Além disso, é interessante notar que, em todos os casos, a unidade de medida é o joule, que homenageia o cientista James Prescott Joule.

Termologia

A termologia é o ramo da Física que estuda a temperatura e seus fenômenos. Dessa maneira, as fórmulas dessa temática dizem respeito às conversões de escalas termométricas. Dessa forma, veja como é essa fórmula:

Conversão entre escalas termométricas

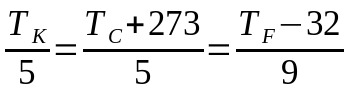
Em que:

• T_K: temperatura na escala Kelvin
• T_C: temperatura na escala Celsius
• T_F: temperatura na escala Fahrenheit

Nesse caso, a escolha dos termos a serem usados pode fazer com que não se use a equação inteira. Ou seja, se for necessário converter da escala Celsius para a escala Fahrenheit, pode-se ignorar o termo referente à escala Kelvin e vice-versa.

Dilatação linear

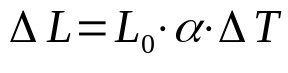
Em que:

• ΔL: variação do comprimento (m)
• L₀: comprimento inicial (m)
• α: coeficiente de dilatação linear (°C^-1)
• ΔT: variação da temperatura (°C)

Quando a temperatura de um corpo varia, seu tamanho também varia. Isso acontece devido a diversos fatores. Por exemplo, o grau de agitação das moléculas dentro do próprio corpo. No caso da dilatação linear, apenas uma dimensão é considerada.

Dilatação superficial

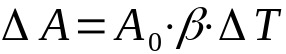
Em que:

• ΔA: variação da área (m²)
• A₀: área inicial (m²)
• β: coeficiente de dilatação superficial (°C^-1)
• ΔT: variação da temperatura (°C)

A dilatação superficial, ou dilatação por área, considera duas dimensões. Devido a isso, as unidades de medida são referentes a área. Além disso, a relação entre o coeficiente de dilatação linear e o coeficiente de dilatação superficial é a de que: 2α = β.

Dilatação volumétrica

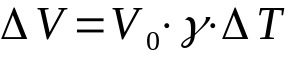
Em que:

• ΔV: variação do volume (m³)
• V₀: volume inicial (m³)
• γ: coeficiente de dilatação superficial (°C^-1)
• ΔT: variação da temperatura (°C)

Quando um corpo possui três dimensões e sua temperatura se altera, deve-se considerar a dilatação volumétrica. Essa relação vale apenas para sólidos. No caso dos líquidos, deve-se considerar, também, a dilatação do recipiente em que ele se encontra. Além disso, a relação entre o coeficiente de dilatação linear e o coeficiente de dilatação superficial é a de que: 3α = γ.

Nas escalas termométricas, é importante notar que apenas as escalas Celsius e Fahrenheit têm unidades de medida lidas como “graus celsius” ou “graus fahrenheit”. No caso da escala Kelvin, não se fala “graus Kelvin”. Além disso, a escala de temperatura absoluta e com unidade fundamental no Sistema Internacional de Unidades é a escala Kelvin.

Calorimetria

A calorimetria diz respeito ao calor e seus efeitos. Dessa maneira, deve-se notar a diferenciação entre o calor e a temperatura. O primeiro é a energia térmica em trânsito no universo. Já a temperatura tem relação com o grau de agitação das moléculas e a energia interna de um corpo.

Calor Latente

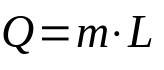
Em que:

• Q: quantidade de calor (J)
• m: massa (kg)
• L: Calor latente (J/kg)

Quando uma determinada substância chega a um ponto de mudança de fase, sua temperatura se mantém constante. Dessa forma, toda energia recebida pelo corpo é usada para a mudança de estado físico. Por conta disso, essa equação não depende da variação de temperatura.

Calor sensível

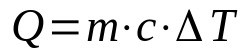
Em que:

• Q: quantidade de calor (J)
• m: massa (kg)
• c: calor sensível (J/K·kg)
• ΔT: variação da temperatura (K)

Essa equação é usada quando a substância não muda de estado. Dessa maneira, sua temperatura pode variar até se atingir um ponto de transição. Além disso, o calor sensível é uma característica intrínseca de cada substância e significa a quantidade de energia necessária para variar a temperatura daquela substância.

As unidades de medida apresentadas nessa temática estão todas conforme o Sistema Internacional de Unidades. Contudo, também há as unidades usuais para a calorimetria. São elas: caloria (para calor e energia), gramas (para massa) e grau celsius (para temperatura).

Termodinâmica

A termodinâmica é a área da Física que estuda as relações entre calor, trabalho e outras formas de energia. Em específico, a transformação de um tipo de energia em outro. As fórmulas dessa temática dizem respeito à primeira lei da termodinâmica, rendimento de uma máquina térmica e a equação de Clapeyron. Veja:

Equação de Clapeyron

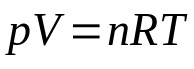
Em que:

• p: pressão do gás (Pa)
• V: volume do gás (m³)
• n: número de mols
• R: constante dos gases ideais (8,3144621 J/K·mol)
• T: temperatura (K)

Essa equação também é conhecida como equação dos gases ideais. Ela relaciona diversas leis físicas para os gases ideais sob diversas condições distintas. Além disso, como o próprio nome diz, ela é válida apenas para gases ideais.

Primeira lei da Termodinâmica

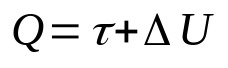
Em que:

• Q: quantidade de calor (J)
• τ: trabalho realizado pelo gás (J)
• ΔU: variação da energia interna (J)

Essa lei é uma consequência do princípio da conservação de energia. Ou seja, a energia total de um sistema sempre será constante. Além disso, pode-se entender essa relação matemática como o calor fornecido a um sistema será convertido em trabalho e na variação da energia interna.

Rendimento de uma máquina térmica

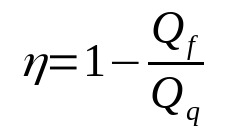
Em que:

• η: rendimento
• Q_f: calor na fonte fria (J)
• Q_q: calor na fonte quente (J)

Note que o rendimento é uma grandeza adimensional. Além disso, ele nunca será igual a 1. Dessa forma, ele estará sempre entre 0 e 1. Isso acontece porque nenhuma máquina térmica real terá rendimento de 100%.

A fórmula do rendimento é uma consequência direta de um dos enunciados da segunda lei da Termodinâmica, que não possui uma fórmula específica relacionada a ela. Além disso, ao manipular as interações entre as partes de uma determinada máquina térmica é possível obter outras equações para o rendimento.

Óptica

A óptica geométrica estuda como a luz interage com os corpos. As equações dessa temática dizem respeito à formação de imagens em uma lente ou em um espelho esférico e quando acontece a refração da luz. Veja as principais fórmulas de óptica:

Lei de Snell-Descartes

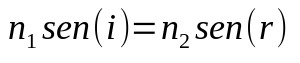
Em que:

• n₁: índice de refração do meio 1
• n₂: índice de refração do meio 2
• sen (i) : seno do ângulo de incidência
• sen (r) : seno do ângulo de refração

Quando a luz troca de meio, sua velocidade também muda. Essa mudança na velocidade pode fazer com que ela mude direção. Por isso, essa fórmula auxilia na determinação de qual será esse ângulo ou qual é o índice de refração do meio.

Lei de Gauss

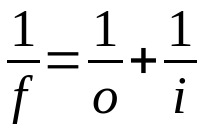
Em que:

• f: distância focal
• o: distância do objeto até a lente
• i: distância da lente até a imagem

Essa equação vale tanto para as lentes quanto para os espelhos. Dessa maneira, deve-se usar a mesma unidade de medida para os três termos. Além disso, note o sinal adotado para cada variável. Se for uma variável real, seu valor deve ser positivo. Caso ela seja virtual, seu valor deve ser negativo.

Aumento linear transversal

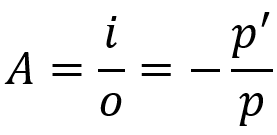
Em que:

• A: aumento linear
• i: tamanho do objeto
• o: tamanho da imagem
• p: distância do objeto
• p’: distância da imagem

Essa equação diz qual será o tamanho da imagem em relação ao objeto. Assim como a equação de Gauss, essa fórmula também vale para a espelhos esféricos quanto para as lentes esféricas.

As equações da óptica dizem respeito às relações geométrica dos caminhos que os raios de luz têm ao incidir sobre espelhos e lentes. No caso da óptica física, seus conceitos são relacionados às fontes de luz e à ondulatória.

Eletrostática

Quando se estuda cargas em repouso, existem relações matemáticas que descrevem essa temática, que é a eletrostática. Sua área de estudo diz respeito às interações entre cargas elétricas e quantidade de cargas em um corpo. Veja as principais fórmulas da Física para esse conteúdo:

Lei de Coulomb

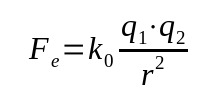
Em que:

• F_e: força elétrica (N)
• k₀: constante eletrostática do vácuo (9 x 10⁹ Nm²/C²)
• q₁: carga elétrica (C)
• q₂: carga elétrica (C)
• r: distância entre as cargas (m)

Essa lei também é chamada de força elétrica. Ela foi baseada na lei da Gravitação de Newton. Por isso, ela é uma relação matemática que depende do inverso do quadrado da distância entre os corpos.

Campo elétrico

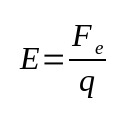
Em que:

• F_e: força elétrica (N)
• q: carga elétrica (C)
• E: campo elétrico (N/C)

Atualmente, a comunidade científica assume que a interação elétrica acontece por meio de entes matemáticos: os campos elétricos e magnéticos. Dessa forma, para a teoria aceita atualmente, o campo elétrico é a medida de como uma carga pode interagir com o espaço à sua volta.

A eletrostática foi desenvolvida tendo como meio interagente o éter. Contudo, o resultado negativo do experimento de Michelson e Morley fez com que a nomenclatura fosse alterada para vácuo.

Eletricidade

O estudo da eletricidade diz respeito à maneira como as cargas elétricas se comportam dentro de fios. No Ensino Médio, é mais comum estudar as Leis de Ohm. Elas estabelecem uma forma de calcular a resistência de um determinado material:

Primeira Lei de Ohm

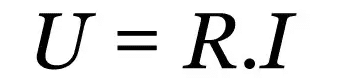
Em que:

• R: resistência elétrica (Ω)
• I: corrente elétrica (A)
• U: tensão elétrica (V)

Essa lei é uma relação empírica que descreve o comportamento de diversos materiais condutores. Independente de qual seja o valor da corrente elétrica, haverá um valor constante que se opõe ao fluxo da corrente. Esse valor é a resistência elétrica.

Segunda Lei de Ohm

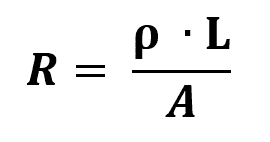
Em que:

• R: resistência elétrica (Ω)
• l: comprimento do resistor (m)
• A: área da espessura do resistor(m²)
• ρ: resistividade do material (Ω/m)

A resistividade de um material é a medida física que se opõe à passagem da corrente. Em linhas gerais, quanto maior for a resistividade, menos condutor o material será. Dessa maneira, o condutores elétricos possuem a resistividade muito baixa.

Além das fórmulas das leis de Ohm, também é possível obter uma relação para a associação de resistores. A qual pode acontecer em série ou em paralelo. Ademais, é preciso notar que todas essas fórmulas de eletricidade são válidas em circuitos sob a ação de uma corrente elétrica contínua. O estudo da corrente alternada requer um formalismo matemático maior.

Vídeos sobre fórmulas da física

As fórmulas da Física são importantes para compreender matematicamente qual fenômeno será estudado. Contudo, pode ser difícil entendê-las apenas com o conteúdo teórico. Dessa maneira, para fixar o que foi aprendido hoje, assista aos vídeos selecionados:

Fórmulas de Física que mais caem no Enem

A Física pode ser um assunto que assusta diversas pessoas. Porém, em avaliações como o Enem, parte dos conteúdos não são cobrados. Dessa maneira, o canal do Umberto Mannarino mostra quais são as principais fórmulas de Física do Enem. Além disso, o youtuber também dá uma breve explicação sobre cada uma delas.

Como calcular a carga elétrica

Para o estudo da eletrostática, é preciso compreender como calcular a carga elétrica. Por isso, o professor Marcelo Boaro explica como fazer essa conta. Além disso, o docente também define o que é esse ente físico e conta por que ele é importante para a eletrostática. Ao fim da aula, Boaro resolve um exercício de aplicação.

Fórmula da velocidade média

Uma das fórmulas mais básicas da Física é a da velocidade média. Ela é um dos pontos iniciais do estudo da cinemática. Por isso, é importante conhecê-la a fundo para entender bem os próximos conceitos. Para saber calcular a velocidade média, assista ao vídeo do professor Marcelo Boaro.

As fórmulas de Física são apenas uma parte de seu estudo. Porém, a preparação para provas de grande escala envolve a compreensão dessas relações quantitativas. Além disso, apesar do futuro incerto do maior exame do Ensino Médio já criado, devido ao desmonte planejado pela gestão Federal entre os anos de 2018 e 2022, é importante conhecer também os assuntos que mais caem no Enem.

Referências