As retas são linhas formadas por pontos e sem espaço entre eles. Elas devem ser infinitas e ilimitadas. Esse conceito é fundamental para o estudo da geometria analítica e da geometria plana. Veja a seguir a definição, a equação, as propriedades e as posições relativas de uma reta.
Publicidade
O que é reta
Uma reta, por definição, é uma linha infinita e ilimitada composta por infinitos pontos alinhados. A sua representação geométrica deve conter setas em ambos os lados para representar sua infinitude. Os pontos da reta devem ser denotados por letras latinas maiúsculas. Já as retas devem ser representadas por letras latinas minúsculas.
Relacionadas
Equação da reta
Caso uma reta seja representada no plano cartesiano, ela possuirá uma equação, chamada de equação geral da reta. Ela dependerá das coordenadas verticais e horizontais. Matematicamente:
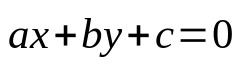
Em que:
- a: constante, deve ser um número real e diferente de zero
- b: constante, deve ser um número real e diferente de zero
- c: constante, deve ser um número real
- x: coordenada do eixo x
- y: coordenada do eixo y
Essa equação vale para qualquer posição de reta no plano cartesiano.
Publicidade
Equação reduzida da reta
Se a reta cruzar a origem do plano cartesiano, ela possuirá um coeficiente angular e um coeficiente linear. Dessa forma:
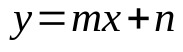
Em que:
Publicidade
- n: coeficiente linear
- m: coeficiente angular
- x: coordenada do eixo x
- y: coordenada do eixo y
Note que o ponto de intersecção deve ser o ponto P (0,n). Dessa forma é possível encontrar os coeficientes angulares e lineares.
Propriedades da reta
Assim como outros entes matemáticos, existem diversas propriedades que ajudam a delimitar o que é uma reta:
- Elas são infinitas;
- Possuem apenas uma dimensão, ou seja, são unidimensionais;
- São compostas por infinitos pontos.
Essas propriedades ajudam a determinar as posições relativas entre as retas e um plano. Confira a seguir mais sobre a posição de uma reta.
Posição da reta
Por estarem no espaço, existem diversas maneiras dos elementos geométricos se posicionarem entre si. Veja a seguir quais são elas:
Paralelas
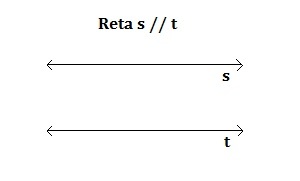
Não há ponto comum entre elas. Isto é, elas ficam lado a lado e sempre estão no mesmo sentido. Para denotar essa posição relativa, usa-se o símbolo //, o qual se lê “paralelo a”.
Perpendiculares
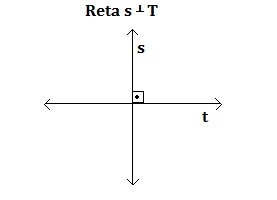
Nesse caso, há apenas um ponto em comum e o ângulo entre elas é um ângulo reto. Ou seja, de 90°. O símbolo para representar essa posição relativa é o ⊥, qual deve ser lido como “perpendicular a”.
Concorrentes
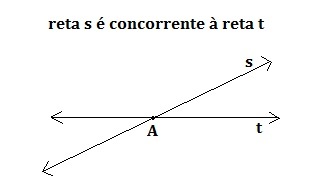
Elas também possuem um ponto em comum, porém não fazem um ângulo reto entre si. A soma dos ângulos entre ambas deve ser igual a 180°. Isto é, eles devem ser suplementares.
Coincidentes

Elas devem possuir todos os pontos em comum. Isso faz com que elas sejam iguais e coincidentes. O símbolo para demonstrar essa posição relativa é o =, que pode ser lido como “igual a” ou “coincidente a”.
Transversais
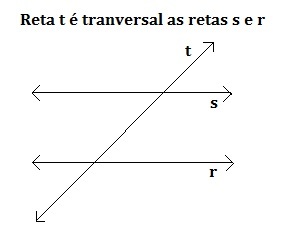
Quando uma reta se cruza com duas ou mais em pontos diferentes, ela é chamada de transversal.
Coplanares
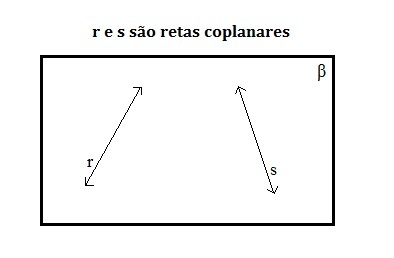
Elas são coplanares quando são pertencentes ao mesmo plano. Isso acontece independente da posição relativa entre elas.
Reversas
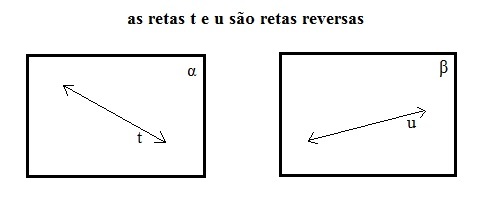
Diferentemente das coplanares, esse tipo de reta deve estar em planos distintos. Isso acontecerá independente da posição relativa entre os planos.
A partir das posições relativas é possível compreender como os elementos geométricos podem interagir entre si. Continue a leitura para entender como esse objeto matemático se comporta no espaço geométrico.
Tipos de reta
Caso a reta esteja sozinha no espaço, é possível que existam três tipos. Veja abaixo quais são elas:
Horizontal

Em um plano cartesiano, sua orientação será paralela ao eixo x. Ou seja, ela deve estar orientada na horizontal.
Vertical
Ao contrário da horizontal, essa reta deve estar orientada paralela ao eixo y. Isto é, sua orientação é vertical.
Inclinada
Quando a orientação não é paralela a nenhum dos eixos coordenados, a reta é considerada inclinada.
Dessa forma, é possível observar que os diferentes tipos de reta se comportam de maneira diferente em um determinado espaço geométrico.
Segmento de reta
O segmento de reta é uma pequena porção de um todo. Ele é delimitado por dois pontos contidos na reta. Além disso, ele é representado pelas duas letras que denotam os pontos e com um traço acima de ambas.
Vídeos sobre retas
Na hora de estudar geometria, seja ela espacial ou analítica, é preciso muita atenção. Afinal, esse conteúdo pode ser muito abstrato. Então, assista aos vídeos selecionados e aproveite para sanar as suas dúvidas:
Posição relativa entre retas
Em um determinado espaço geométrico, as retas podem ter posições relativas entre si. Nesse vídeo, a professora Gis explica todas essas posições e dá exemplos em cada um dos casos, facilitando a compreensão. Confira!
Diferença entre reta, semirreta e segmento de reta
Aqui, a professora Gis ensina a diferenciar três elementos fundamentais da geometria, são eles: a reta, a semirreta e o segmento de reta. Para isso, a professora define e demonstra graficamente o que é cada um desses entes matemáticos.
Equação geral da reta
O estudo da geometria analítica aplica os conhecimentos matemáticos aos conceitos de geometria espacial. Isso pode parecer assustador à primeira vista. Então, confira o macete do professor Paulo Pereira, do canal Equaciona, para compreender a equação geral da reta de uma vez por todas!
A geometria é uma importante área da Matemática. Por conta disso, seus conceitos são muito cobrados em provas de grande escala, como os vestibulares e o Enem. Aprofunde seus conhecimentos sobre a geometria analítica e entenda o que é a equação da reta.
Referências
Geometria Analítica: Um tratamento vetorial (2004) – Paulo Boulos & Ivan Camargo.
Geometria Analítica (1995) – Alfredo Steinbruch & Paulo Winterle.
Vetores e geometria analítica (2014) – Paulo Winterle.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Retas. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/retas. Acesso em: 03 de January de 2025.
1.
A respeito das dimensões necessárias para existência de uma reta, assinale a alternativa correta:
a) As retas são figuras adimensionais, ou seja, sua dimensão é zero. Isso acontece porque as retas são conjuntos de pontos, e os pontos são figuras que não possuem dimensão.
b) As retas são figuras unidimensionais, ou seja, existem em uma única dimensão.
c) As retas são as únicas figuras unidimensionais que existem.
d) As retas são bidimensionais. Assim, é possível medir tanto o comprimento quanto a largura de figuras sobre uma reta.
e) As retas são figuras tridimensionais, por isso, é possível encontrar retas no espaço tridimensional.
Alternativa correta: B
Por definição, as retas devem possuir apenas uma dimensão. Dessa forma, elas devem ser figuras unidimensionais.
2.
Sobre as classificações possíveis entre retas, também conhecidas como posições relativas entre duas retas, assinale a alternativa correta:
a) Retas perpendiculares são as concorrentes que formam pelo menos um ângulo reto. Quando isso acontece, todos os ângulos no encontro também são de 90°.
b) Retas concorrentes são as que possuem dois pontos de encontro. Quando isso acontece, podemos dizer que essas retas possuem todos os pontos comuns e, por isso, são concorrentes.
c) Retas perpendiculares são aquelas que possuem apenas um ponto de encontro.
d) Retas paralelas só se encontram nas proximidades do infinito.
e) Retas concorrentes encontram-se em apenas um ponto, formando um ângulo qualquer, exceto o ângulo reto. Para os casos em que esse ângulo é formado, as retas recebem o nome de perpendiculares.
Alternativa correta: A
As retas perpendiculares devem ser concorrentes. Porém, o ângulo formado entre elas deve ser de, exatamente, 90°.