Quando nos referimos aos múltiplos e aos divisores de um número, estamos falando em MMC e MDC, como são conhecidos no estudo da matemática básica. O MDC é bastante útil quando vamos realizar somas ou subtrações em frações, já que se faz necessário encontrar um denominador em comum para o processo. É importante frisar, entretanto, que não é essencial que o denominador seja o MMC, porém a escolha desse número facilitará e muito o cálculo desejado.
Publicidade
MMC é a sigla usada para Mínimo Múltiplo Comum, enquanto MDC é Mínimo Divisor Comum, e o cálculo usado para ambos é bastante semelhante, apesar de existirem algumas variações no que se refere a esse objetivo. O MMC e o MDC podem ser resolvidos por meio da fatoração e, por isso, vamos retomar o aprendizado relacionado a esse componente da matemática.
Puxando da memória o que é a fatoração de dois ou mais números, e como fazê-la, temos que lembrar do passo a passo para que se encontre os resultados corretamente. O primeiro passo é fazer um grande traço vertical onde, à esquerda, deverão ser colocados os números que precisamos fatorar, enquanto à direita, escrevemos o menor número primo que pode dividir um dos números da esquerda. Em seguida, devemos tentar dividir todos os números da esquerda pelo que está à direita. Quando for divisível, devemos colocar o quociente na linha de baixo, e caso não seja, repetimos o número. O processo deve ser repetido até que se encontre apenas o “1” repetido no lado esquerdo. Ficou difícil visualizar? Confira a imagem abaixo:
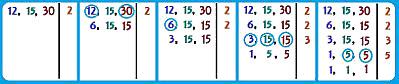
Acima, fizemos a fatoração dos números 12, 15 e 30, e a partir disso, podemos encontrar o MMC e o MDC. Para encontrar o MMC, devemos fazer a multiplicação dos números aos quais chegamos do lado direito do traço. Confira: MMC (12, 15, 30) = 2 . 2 . 3 . 5 = 60. Temos, portanto, que o Mínimo Múltiplo Comum entre esses números é 60.
Em contrapartida, quando queremos encontrar o MDC entre 12, 15 e 30, devemos ver quais dos números obtidos ao lado direito do traço que passou por divisão com todos os números de uma única vez ao lado esquerdo. Nesse caso, temos somente o número 3, de forma que: MDC (12, 15, 30) = 3.
Referências
Matemática – Curso Completo – Valter dos Santos Fernandes, Jorge Daniel Silva, Orlando Donisete Mabelini

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. MMC e MDC. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/mmc-e-mdc. Acesso em: 02 de January de 2026.
01. [FUVEST] No alto da torre de uma emissora de televisão, duas luzes “piscam” com frequências diferentes. A primeira “pisca” 15 vezes por minuto e a segunda “pisca” 10 vezes por minuto. Se num certo instante, as luzes piscam simultaneamente, após quantos segundos elas voltarão a “piscar simultaneamente”?
a) 12
b) 10
c) 20
d) 15
e) 30
02. [MACKENZIE] Nas últimas eleições, três partidos políticos tiveram direito, por dia, a 90 s, 108 s e 144 s de tempo gratuito de propaganda na televisão, com diferentes números de aparições. O tempo de cada aparição, para todos os partidos, foi sempre o mesmo e o maior possível. A soma do número das aparições diárias dos partidos na TV foi de:
01. [Como o exercício nos questiona “após quantos segundos elas voltarão a ‘piscar simultaneamente’”, precisamos converter as informações dadas para medidas de “segundos”. Portanto, se a primeira torre “pisca” 15 vezes por minuto, sabendo que um minuto equivale a 60 segundos, podemos fazer 60 : 15 = 4, pois as luzes da primeira piscam de 4 em 4 segundos. Equivalentemente, os cálculos para a segunda torre são 60 : 10 = 6, o que nos indica que as luzes da segunda torre piscam de 6 em 6 segundos.
4, 6 | 2
2, 3 | 2
1, 3| 3
1, 1 | 3 * 2* 2 = 12
Multiplicando os números que dividem o 4 e o 6, temos 2 x 1 x 3 = 12. Portanto, MMC (4,6) = 12. Logo, as torres piscaram juntas a cada 12 segundos. Por isso, corresponde à letra A]
02. [Para resolver essa questão, precisamos recorrer à ideia do Máximo Divisor Comum, pois queremos que o tempo de cada aparição seja o maior possível.
Façamos então a fatoração simultânea dos tempos de aparição de cada político:
90, 108, 144 | 2
45, 54, 72 | 2
45, 27, 36 | 2
45, 27, 18 | 2
45, 27, 9 | 3
15, 9, 3 | 3
5, 3, 1 | 3
5, 1, 1 | 5
1, 1, 1 |
Já que estamos procurando o MDC, vamos procurar aqueles números que dividiram os três números ao mesmo tempo. Fazendo a multiplicação deles, temos: 2 x 3 x 3 = 18.
Encontramos o tempo de aparição de cada político, 18 segundos. Precisamos agora descobrir quantas aparições cada um deles realizou. Vejamos:
90: 18 = 5 aparições
108/18 = 6 aparições
144 : 18 = 8 aparições
Somando as aparições de cada um, encontramos 5 + 6 + 8 = 19 aparições.]