Soma e produto é um método usado para calcular as raízes da equação do 2° grau, sendo, portanto, uma variação da fórmula de Bhaskara. Esse método estabelece duas relações entre as raízes e os coeficientes da equação. Quando dois números que satisfaçam as duas relações simultaneamente forem encontradas, isso significa que encontramos as raízes de determinada equação.
Publicidade
Como já sabemos, a forma geral da equação de 2° grau é ax² + bx + c = 0. Diante disso, vamos entender como funciona esse método de cálculo.
Como funciona o método da soma e produto?
O método é feito por meio de uma fórmula constituída por duas relações que devem ser satisfeitas. Considerando que x1 e x2 são as duas raízes da equação, temos então a fórmula:
x_1+ x_2= -b/a
x_1.x_2= c/a
Para resolver, precisamos encontrar dois números que satisfaçam as duas relações acima. Para resolver a equação de 2° grau usando este método, você deve, primeiro, encontrar os dois números que atendam a relação. Mesmo que hajam inúmeras possibilidades, em exercícios, normalmente, essas são limitadas. Foque inicialmente no produto, e então descubra, depois, se satisfaz também a soma.
Confira o exemplo abaixo para melhor entendimento:
X² – 5x + 6 = 0
Ao observarmos a equação acima, podemos tirar dela os coeficientes, sendo eles:
A = 1
B = -5
C = 6.
Publicidade
Diante disso, precisamos aplicar a regra de soma e produto. A soma das raízes é 5, e o produto é 6, de forma que precisamos encontrar dois números que tenham a soma igual a 5 e o produto igual a 6. As únicas duas possibilidades são 2 e 3. Confira abaixo a resolução:
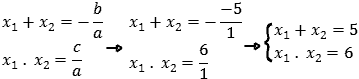
![]()
Publicidade
Referências
Matemática – Valter dos Santos Fernandes, Jorge Daniel Silva, Orlando Donisete Mabelini

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Soma e produto. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/soma-e-produto. Acesso em: 26 de April de 2025.
01. [Fuvest] Se m e n são raízes de x² – 6x + 10 = 0, então 1/m + 1/n vale :
a)6
b)2
c)1
d)3/5
e)1/6
02. [Mackenzie] Sejam a e b raízes da equação x² – 3kx + k² = 0 tais que a² + b² = 1,75. O valor de k² é :
a)(1,75)²
b)17,5
c)175
d)0,5
e)0,25
01. [D]
02. [E]