Velocidade angular é a grandeza que mede a distância angular percorrida em um determinado intervalo de tempo. Dessa forma, as velocidades linear e angular podem ser relacionadas porque ambas descrevem a variação do espaço em um intervalo de tempo. Continue a leitura para saber mais sobre o assunto.
Publicidade
O que é a velocidade angular
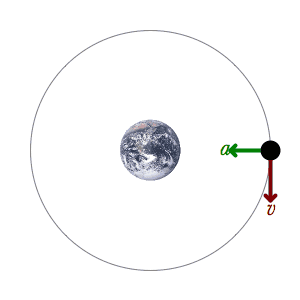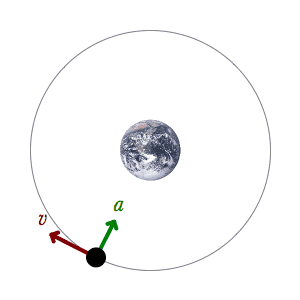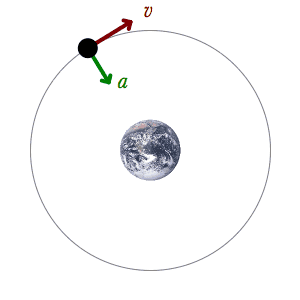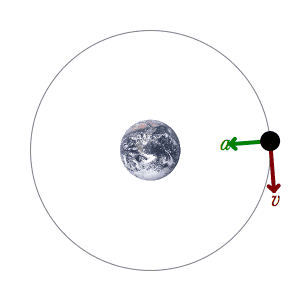
Velocidade angular é a taxa de variação do deslocamento angular no tempo. Dessa forma, ela pode ser análoga à velocidade linear. Mesmo que um corpo possa ter os dois tipos de velocidade, seus valores serão diferentes. Isso acontece porque o deslocamento angular difere do deslocamento linear. Além disso, a unidade de medida da velocidade angular é radianos por segundo (rad/s).
Relacionadas
Outra maneira de relacionar as velocidades linear e angular é que a velocidade linear é o produto do raio pela componente angular da velocidade. Com isso, para que as velocidades angulares sejam iguais, quanto maior for o raio, maior deverá ser a velocidade linear.
Fórmula da velocidade angular
De maneira análoga à velocidade linear, deve-se relacionar a variação do espaço com o tempo decorrido. Contudo, a diferença é que o espaço considerado será um espaço angular. Além disso, por convenção, o sentido positivo do movimento acontece no sentido horário. Logo, se o movimento for em sentido anti-horário, ele será negativo.
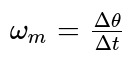
- ωm: velocidade angular média (rad/s)
- Δθ: deslocamento angular (rad)
- Δt: intervalo de tempo (s)
O deslocamento angular e o intervalo de tempo são dados pela subtração entre as grandezas finais pelas iniciais. Ou seja, no caso do deslocamento angular é dado por: Δθ = θf – θi. Dessa forma, o intervalo de tempo é: Δt = tf – ti. Além disso, a relação entre velocidade linear e angular é dada por: v = ωR. Onde v é a velocidade linear e R é o raio da circunferência.
Publicidade
Vídeos sobre velocidade angular
Compreender os conceitos do movimento circular pode parecer que você está rodando sobre o mesmo ponto. Porém, para que o aumento do seu conhecimento seja linear, selecionamos videoaulas sobre esse assunto. Então, acompanhe nossa seleção.
Movimento circular uniforme
A cinemática do movimento circular uniforme é um pouco mais complexa. Isso acontece porque os conceitos das grandezas angulares são inseridos. Dessa forma, para facilitar a visualização de tais conhecimentos físicos, os professores Claudio Furukawa e Gil Marques realizam experimentos sobre o movimento circular uniforme.
Publicidade
Grandezas angulares
As grandezas angulares são um pouco diferentes das grandezas lineares. Por isso, o professor Marcelo Boaro explica a relação entre elas. Além disso, ao fim da videoaula, o docente resolve um exercício de aplicação sobre esse tema.
Estudo do movimento circular
O professor Marcelo Boaro explica todas as equações do movimento circular uniforme. Dentre elas, está a velocidade angular. Portanto, durante o vídeo, Boaro explica, também, a relação entre as grandezas lineares e angulares. Por fim, o professor realiza um exercício sobre o tema.
O movimento circular é uma área da Física que é muito cobrada em provas de grande escala. Por exemplo, Enem e vestibulares. Por isso, aprofunde ainda mais seu conhecimento estudando sobre o momento angular.
Referências
YOUNG, H. D. et al. Física I: Mecânica. São Paulo: Addison & Wesley. 2016
HALLIDAY, D. et al. Física: Volume 1. Rio de Janeiro: Pearson. 2008
NUSSENZVEIG, H. D. Curso de Física Básica: Volume 1. Rio de Janeiro: Blucher. 2014

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Velocidade angular. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/velocidade-angular. Acesso em: 25 de April de 2025.
1. [Mackeinze]
Devido ao movimento de rotação da Terra, uma pessoa sentada sobre a linha do Equador tem velocidade escalar, em relação ao centro da Terra, igual a:
Adote: Raio equatorial da Terra: 6300 km. π = 22/7
a) 2250 Km/h
b) 1650 Km/h
c) 1300 Km/h
d) 980 Km/h
e) 460 Km/h
Alternativa correta: B
Sabe-se que a velocidade angular de uma rotação completa pode ser dada por: ω = 2π/T
Assim, temos:
v = ωR
v = 2πR/T
Sabemos que a rotação da Terra é 24h.
Substituindo os valores dados pelo exercício encontramos que a velocidade é:
v = 1650 km/h
2. [IF-GO]
Podemos dizer que uma partícula se encontra em movimento quando suas posições sofrem alterações no decorrer do tempo em relação a um dado referencial. Estando em movimento, ainda podemos dizer que a partícula pode estar em movimento uniforme ou em movimento variado. Acerca de um satélite geoestacionário que se encontra sobre a linha do equador terrestre, podemos afirmar corretamente que
a) não possui aceleração pelo fato de sua velocidade ter módulo constante.
b) a aceleração tangencial é nula e a aceleração centrípeta dependerá da altitude que se encontrar em relação à superfície da Terra.
c) possui aceleração escalar constante e diferente de zero.
d) sua aceleração resultante é a própria aceleração tangencial.
e) a aceleração vetorial desse satélite não pode ser nula, pois o satélite deverá possuir velocidade tangencial muito grande.
Alternativa correta: B
A velocidade linear de um satélite geoestacionário é constante. Logo, o módulo da velocidade linear não muda, porque a aceleração tangencial é nula.
A aceleração centrípeta, por sua vez, não é nula, porque há mudança de direção no vetor velocidade. Logo, a aceleração do satélite depende da altitude na qual ele se encontra.