Somar vetores pode ser útil para resolver diversos problemas de Física. Por exemplo, problemas envolvendo diversas forças atuando em um corpo ou problemas de cinemática. Portanto, nesse post você aprenderá o que é soma de vetores, para que serve a soma de vetores e muito mais. Confira:
Publicidade
O que é soma de vetores?
Um vetor é um ente matemático que possui módulo, direção e sentido. Além disso, é possível realizar operações com tais entes matemáticos. Portanto, quando nos referimos à soma ou adição de vetores, obteremos outro vetor como resultado. Este é o chamado vetor resultante.
Relacionadas
Existem duas maneiras de fazer o cálculo de vetores: a adição gráfica, também chamada de adição geométrica, e a adição por decomposição, também chamada de adição algébrica.
Para que serve a soma de vetores
Em Física, a soma de vetores é muito utilizada na análise de grandeza que dependem da direção e do sentido do movimento. Por exemplo: a análise da velocidade de um corpo, o cálculo da estática de um objeto, a maneira com a qual duas ou mais cargas interagem entre si etc.
Adição Gráfica
A adição gráfica (ou geométrica) de vetores pode ser feita de duas maneiras: por meio da regra do polígono e pela regra do paralelogramo. Assim, qualquer uma das duas formas são equivalentes. Isto é, ambas maneiras podem ser usadas em qualquer caso.
Vetores podem ser representados por meio de letras maiúsculas com uma seta horizontal orientada da esquerda para a direita ou por meio de uma letra maiúscula em negrito. Dessa forma, supondo dois vetores A e B, que, somados, obtém-se o vetor resultante R.
Publicidade
Regra do Polígono
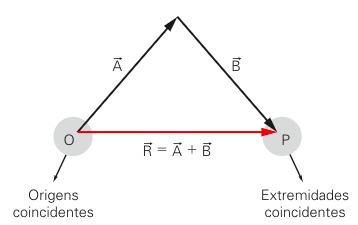
Onde:
- A: vetor A
- B: vetor B
- R = A + B: módulo da soma dos vetores A e B
Para determinar a resultante usando a regra do polígono, transpomos os vetores que desejamos somar e unimos o fim de um vetor com o início do próximo vetor. Isso pode ser feito com quantos vetores forem necessários. Logo, vetor resultante deve fechar o polígono com origem coincidente com o vetor A e extremidade no vetor B.
Regra do Paralelogramo
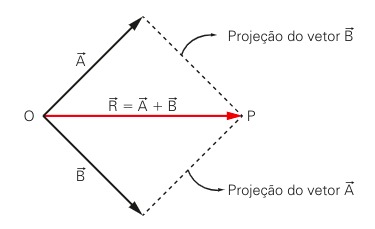
Onde:
Publicidade
- A: vetor A
- B: vetor B
- R = A + B: módulo da soma dos vetores A e B
A fim de determinar a soma de vetores usando a regra do paralelogramo devemos unir a origem de dois vetores e projetar paralelamente um vetor nas extremidades. Dessa maneira, haverá um paralelogramo. Então, o vetor resultante tem origem coincidente com os vetores somados e sua extremidade será no ponto onde as projeções se encontram.
Note que a regra do paralelogramo deve ser aplicada em dois vetores por vez.
Cálculo da intensidade por meio da decomposição
A soma de vetores de maneira algébrica acontece de duas maneiras: usando a lei dos cossenos ou a lei dos senos. Assim, a primeira forma de cálculo é utilizada quando a regra do paralelogramo é aplicada. Já a segunda regra é usada quando aplica-se a regra do polígono. Contudo, a soma algébrica serve para calcular a intensidade (módulo) de vetores.
Lei dos cossenos
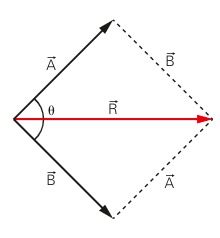
Conhecendo o valor do ângulo formado entre os vetores somados, torna-se válida a lei dos cossenos, a qual, matematicamente é da forma:
![]()
Onde:
- R : intensidade do vetor resultante
- A: módulo do vetor A
- B: módulo do vetor B
- cos θ: cosseno do ângulo formado entre os vetores A e B
Note que, caso o ângulo formado entre os vetores for 90°, a lei dos cossenos será igual ao teorema de pitágoras, porque cos 90° = 0.
Lei dos senos
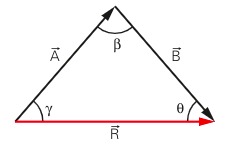
Quando aplica-se a regra do polígono é possível obter o vetor resultante por meio da lei dos cossenos, a qual, matematicamente é da forma:
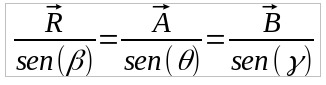
Onde:
- R : intensidade do vetor resultante
- sen θ: seno do ângulo formado entre os vetores B e R
- A: intensidade do vetor A
- B: intensidade do vetor B
- sen γ: seno do ângulo formado entre os vetores A e R
- sen β: seno do ângulo formado entre os vetores A e B
A lei dos senos é muito utilizada no estudo da estática do ponto material ou quando não se conhece a intensidade de um dos vetores somados.
Vídeos sobre Soma de Vetores
Agora que você já aprendeu as maneiras mais recorrentes de fazer a soma de vetores, assista aos vídeos que selecionamos para você aprofundar seus conhecimentos sobre esse assunto. Veja:
Adição de vetores usando o método poligonal
O professor Marcelo Boaro explica como fazer a adição de vetores pro meio do método da poligonal. Além disso, Boaro dá dicas e macetes para a resolução de exercícios sobre esse assunto. Ao fim da videoaula, o professor resolve um exercício de aplicação.
Aprenda a usar a regra do paralelogramo
A regra do paralelogramo parece ser muito complicada de se aplicar. No vídeo do canal Chama o Físico, o professor Thales ensina a usar a regra do paralelogramo. Dessa forma você pode aplicar essa regra sem medo de errar.
Adição de vetores usando a regra do paralelogramo
O método do paralelogramo é uma das maneiras mais comuns de se fazer a soma de vetores. Para explicar e aprofundar nesse conteúdo, o professor Marcelo Boaro explica de maneira descontraída como aplicar essa regra. Ao fim da videoaula, Boaro resolve um exercício de aplicação sobre a regra do parelelogramo.
As operações com vetores são muito importante em diversas áreas da Física e da Matemática. Assim, uma dessas áreas é o estudo do Plano inclinado.
Referências
BOULOS, P. CAMARGO, I. Geometria Analítica – Um tratamento vetorial. São Paulo: Pearson. 2004.
BUENO, L. F. Física: 1º ano. São Paulo: Maxiprint Editora. 2018.
STEINBRUCH, A. WINTERLE, P. Geometria Analítica. São Paulo: Pearson. 1995

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Soma de vetores. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/soma-de-vetores. Acesso em: 02 de April de 2025.
1. [Eear]
Dois vetores V1 e V2 formam entre si um ângulo θ e possuem módulos iguais a 5 unidades e 12 unidades, respectivamente. Se a resultante entre eles tem um módulo igual a 13 unidades, podemos afirmar que corretamente que o ângulo θ entre os vetores V1 e V2 vale:
a) 0°
b) 45°
c) 90°
d) 180°
Alternativa correta:C
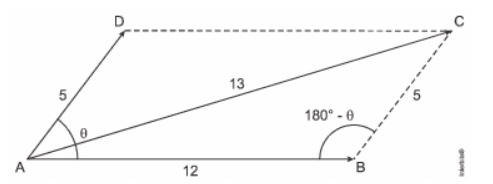
Aplicando a lei dos cossenos e sabendo que cos (180° – θ) = – cos θ, temos:
13² = 5² + 12² – 2*5*12*cos (180-θ)
169 = 25 + 144 + 120 cosθ
cosθ = 0
Logo θ = 90°
2. [Ifsul]
Considere um relógio com mostrador circular de 10 cm de raio e cujo ponteiro dos minutos tem o comprimento do mostrador. Considere esse ponteiro como um vetor de origem no centro do relógio e direção variável.
O módulo da soma vetorial dos três vetores determinados pela posição desse ponteiro quando o relógio marca 12 horas, 12 horas e 30 minutos e por fim 12 horas e 40 minutos é, em cm, igual a:
a) 30
b) 10(1 + 31/2)
c) 20
d) 10
Alternativa correta: D
Somando vetorialmente os três resulta nele mesmo. Isso acontece porque os vetores de 12 horas e 12 horas e 30 minutos se anulam mutualmente na soma. Assim, resta apenas o último vetor apontado às 12 horas e 40 minutos, que possui módulo 10 cm.