Estudamos na geometria os triângulos, e descobrimos que existem muitos formatos e tamanhos, e que suas nomenclaturas se dão a partir de algumas de suas características, como por exemplo os seus ângulos internos. Entre eles, encontramos o triângulo reto. Seu formato é, basicamente, de um ângulo reto, ou seja, de 90°, e outros dois agudos, ou seja, com ângulo menor de 90°. Além disso, soma dos três ângulos internos tem que ser igual a um ângulo raso, equivalente a 180°.
Publicidade
Muito usado para diversos cálculos na matemática, como o cálculo de áreas, de volume e no cálculo algébrico, o triângulo retângulo tem sua área dada pela metade do produto dos menores lados. Além disso, existe uma relação entre os lados e ângulos do triângulo retângulo que são a base da trigonometria. Quando se sabe as medidas de dois dos três lados, ou a medida de um lado e de um ângulo agudo, é possível encontrar as medidas dos outros lados e ângulos.
Quais são os elementos de um triângulo retângulo?
São quatro os principais elementos que formam um triângulo retângulo: os catetos, a hipotenusa, a altura relativa à hipotenusa e as projeções dos catetos. Chamamos de catetos os menores lados do triângulo retângulo, e são eles que formam o ângulo de 90°. A altura relativa à hipotenusa, por sua vez, é a distância que há entre a hipotenusa e o vértice oposto, e o maior lado do triângulo, oposto ao ângulo de 90°, é a hipotenusa. As projeções dos catetos são as duas metades da altura relativa à hipotenusa.
Relações métricas
Os triângulos retângulo apresentam quatro relações métricas. Considerando, no triângulo abaixo, que a é a hipotenusa, h a altura relativa à hipotenusa, c e b são os catetos, temos que a divisão de h de um triângulo retângulo acaba formando mais dois triângulos retângulos.

Com isso, podemos chegar a conclusão que:
c² = m . a e b² = n . a
b. c = a . h
h² = m . n
c² + b² = m . a + n . a
c² + b² = a (m + n) (lembrando que a = m + n)
c² + b² = a . a
c² + b² = a²
Que é o famoso Teorema de Pitágoras: a soma dos quadrados dos catetos é igual ao quadrado da hipotenusa.
Publicidade
A soma dos ângulos internos dos triângulos retângulos sempre será igual a 180°, de forma que podemos dizer que:
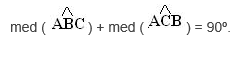
Teorema Linear de Tales
Com o teorema de Tales podemos estabelecer as relações que existem entre os segmentos quando um feixe de paralelas é cortado por duas ou mais transversais, conforme a imagem abaixo.
Publicidade
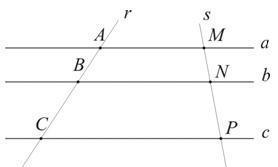
Se considerarmos as linhas a, b e c, paralelas duas a duas, e as transversais r e s, temos que as medidas dos segmentos determinados em r são diretamente proporcionais às medidas dos segmentos correspondentes na reta s.
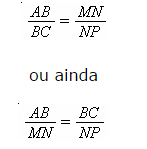
Quando queremos estabelecer as condições de semelhança entre dois triângulos obtidos quando traçamos uma paralela de um lado a outro deles, podemos usar o teorema de tales. Os lados são proporcionais e, portanto, temos dois triângulos semelhantes.
Relações trigonométricas de um triângulo retângulo
Podemos ainda calcular a medida dos lados dos triângulos retângulos por meio da medida de um ângulo e de um lado por meio da trigonometria. Existem três principais relações trigonométricas, que são o Seno, Cosseno e Tangente, adicionados de mais três, a Cotangente, Secanta e Cossecante.
Seno de um ângulo
O seno de um ângulo é dado pela razão entre os lados que formam o ângulo agudo:
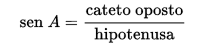
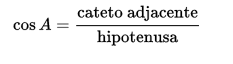
Cosseno de um ângulo
O cosseno, por sua vez, é a razão que há entre a medida do cateto adjacente e a medida da hipotenusa, dado, ainda, pela razão que há entre os lados que formam o ângulo agudo:
Tangente de um ângulo
A tangente é dada pela razão entre o seno e o cosseno de um determinado ângulo, ou ainda entre os catetos:
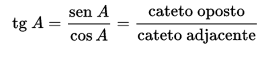 Imagem 6
Imagem 6
Cotangente de um ângulo
A cotangente é dada pela razão entre o cosseno e o seno de um ângulo, ou entre os catetos:
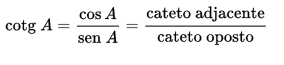
Secante de um ângulo
A secante é dada pelo inverso do cosseno do ângulo, ou ainda entre os lados que o formam:
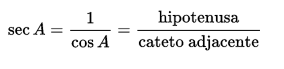
Cossecante de um ângulo
É dada pela relação inversa do seno do ângulo, ou ainda entre os lados que formam o outro ângulo agudo:
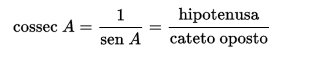
Referências
Fundamentos de matemática elementar 3 – Trigonometria – Gelson Iezzi

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Triângulo retângulo. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/triangulo-retangulo. Acesso em: 03 de April de 2025.
01. [ENEM] Determine os valores de x, y e z em cada caso abaixo:
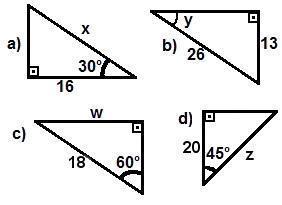
02. [ENEM] Em um triângulo retângulo, determine as medidas dos ângulos agudos e da hipotenusa, sabendo que um dos catetos mede 3 cm e o outro mede √3 cm.
01.



02.

