Equação de Segundo Grau

As expressões matemáticas que apresentam incógnitas, expoentes, coeficientes e sinal de igualdade em sua composição são chamadas de equações, que são caracterizadas pelo maior expoente de uma das incógnitas presentes. Por exemplo, na expressão 2x +2 = 0, a incógnita é x e seu expoente é 1, de forma que essa equação fica denominada uma equação de primeiro grau.

Publicidade

As equações de segundo grau, por sua vez, apresentam em uma das incógnitas o expoente 2, sendo classificada como equação de segundo grau. Um exemplo para melhor entendimento é a equação a seguir: x² + 3x – 5 = 0. A expressão apresenta duas incógnitas x, mas em uma delas o expoente é 2.

Da mesma forma, seguindo o mesmo raciocínio, podemos caracterizar equações de terceiro grau em que o expoente de uma das incógnitas será 3. Por exemplo: x³ + 3x² – x + 5 = 0. Nesse caso, temos três incógnitas, sendo que uma delas apresenta o expoente 3, que é o maior da expressão, tornando-a uma equação de terceiro grau.

Para resolver cada uma dessas equações mencionadas acima, existe uma forma na matemática. Confira a seguir como resolver as equações de segundo grau.

Equações de Segundo Grau

Normalmente se trabalha em cima da Fórmula de Bhaskara para resolver equações de segundo grau, encontrando a sua solução, ou seja, encontrando suas raízes. Chamamos de raízes os valores que satisfazem as equações. Por exemplo, em uma equação como x² – 10x +24, temos duas possibilidades de raízes, que são x = 4 ou x = 6. Se ainda não deu para entender, vamos para o passo a passo a seguir.

Considerando a raiz x = 4, vamos substituir as incógnitas x da equação pelo número 4. Temos que:

X² – 10x + 24 = 0
4² – 10 . 4 + 24 = 0
16 – 40 + 24 = 0
-24 + 24 = 0

Publicidade

E agora substituindo a outra raiz na equação, x = 6, temos:

X² – 10x + 24 = 0
6² – 10 . 6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0

Podemos dizer, portanto, que ambas as raízes permitem que a equação seja verdadeira. Mas como fazemos para encontrar essas raízes para saber quais são os valores perfeitos que satisfazem a essa equação? É aí que entra a fórmula de Bhaskara.

Publicidade

Fórmula de Bhaskara

A fórmula de Bhaskara pode, como mencionamos anteriormente, ser usada para resolver as equações de segundo grau, ajudando-nos a encontrar as raízes para essas equações. Confira abaixo a fórmula de Bhaskara.

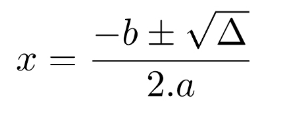
Dentro da raiz quadrada temos o delta, que representa:

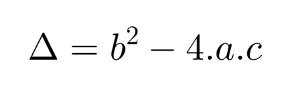
O primeiro passo para resolver a equação é, portanto, encontrar o valor de delta. Considere a seguinte equação para exemplificar a forma como resolvemos equações de segundo grau:

X² – 2x – 3 = 0, sendo que a = 1, b = – 2 e c = -3

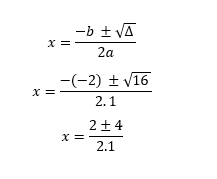
Diante disso, podemos então passar para a fórmula de Bhaskara:

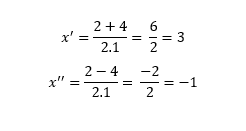
Diante disso, temos duas opções: a operação c-m o mais e a operação com o menos:

x^’=(2+4)/2.1= 6/2=3
x^”=(2-4)/2.1= (-2)/2=-1

Com isso temos que as raízes possíveis para essa equação são x’ = 3 e x’’ = -1

Para tirar a prova real, basta substituir na equação inicial os dois valores:

X² – 2x – 3 = 0
3² – 2 . 3 – 3 = 0
9 – 6 – 3 = 0
9 – 9 = 0

E a outra raiz:

X² – 2x – 3 = 0
-1² – 2 . (-1) – 3 = 0
1 + 2 – 3 = 0
3 – 3 = 0

Referências