Existem situações em que podemos combinar vários itens ou objetos para fazer algo. Por exemplo, com 6 frutas do nosso gosto, podemos fazer uma vitamina escolhendo 2, 3 ou até mesmo 6 delas. Mas como realizar a contagem dessas possibilidades? A combinação é uma maneira de fazer isso. Entenda o que é, conheça a combinação simples e a composta e saiba o que as diferencia do arranjo.
Publicidade
O que é a combinação
Combinação nada mais é do que um meio de contagem em análise combinatória. Existem duas formas de combinação: a simples e a composta. Cada uma possui seu próprio uso e suas características.
Relacionadas
Dentro desse estudo que envolve a análise combinatória, não existe muita teoria. O indicado é resolver bastantes exercícios, para que você entenda o raciocínio por trás deles e a assimilação do conteúdo fique mais fácil. Vamos, então, compreender cada um dos tipos de combinação.
Combinação simples
Vamos retornar ao exemplo das frutas. Suponha que você vá até um lugar onde se vende vitaminas com diferentes frutas. As suas opções são as seguintes: abacate, mamão, banana, maçã, morango e laranja. Porém, dessas 6 escolhas possíveis, você pode combinar dois tipos delas. A tabela a seguir mostra essas possibilidades:
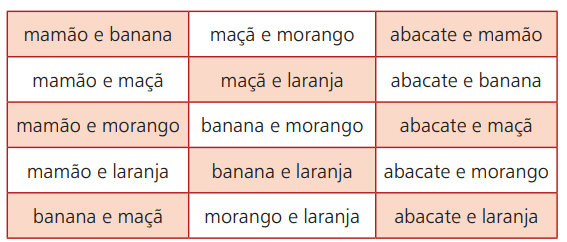
Se você escolher, por exemplo, mamão e laranja, nessa ordem, é o mesmo que escolher laranja e mamão. Isso quer dizer que a ordem em que você escolher as frutas não vai interferir no resultado final. Assim, suas possibilidades de escolha consistirão em um agrupamento não ordenado de duas frutas escolhidas entre as seis possíveis.
Publicidade
Dizemos, então, que cada uma das possibilidades anteriores é uma combinação simples das seis frutas tomadas duas a duas. Em suma, na combinação simples, a ordem não interfere no resultado. Para se realizar a contagem de todas as possibilidades, é utilizada uma fórmula específica, que será apresentada a seguir. De uma maneira mais formal, a combinação simples pode ser definida como:
Dados n elementos distintos, chama-se combinação desses n elementos tomados p a p (com p ≤ n) qualquer subconjunto formado por p elementos distintos, escolhidos entre os n.
Fórmula da combinação simples
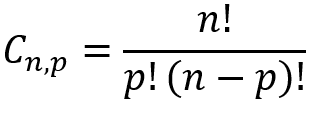
Publicidade
Para entender essa fórmula, vamos utilizar o exemplo anterior. Nesse caso, temos que p=2, pois é a quantidade de elementos possíveis, do subconjunto de frutas escolhidas, para se fazer a vitamina. Além disso, n=6, pois é o número total de frutas disponíveis. Aplicando esses números na fórmula, teremos o seguinte resultado:
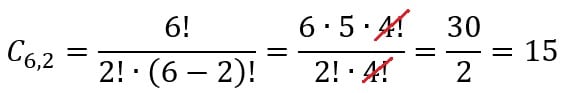
Combinação composta
Essa combinação também é conhecida como sendo combinação com repetição. Em outras palavras, ela é uma combinação em que é possível escolher dois ou mais elementos repetidos do conjunto de possibilidades possíveis. Por exemplo: suponha que você vá até uma sorveteria e deseje comprar um sorvete com quatro sabores, sendo que, na sorveteria, só há 3 sabores disponíveis: chocolate, baunilha e morango. Nesse caso, é possível repetir algum desses sabores.
Fórmula da combinação composta
Existe uma fórmula para calcular o total de possibilidades de uma combinação com repetição. Veja a seguir:
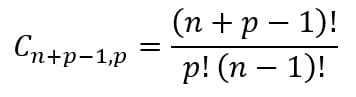
No caso do exemplo da sorveteria, teremos que n=3 e p=4. Substituindo esses valores na fórmula, iremos obter o seguinte resultado:
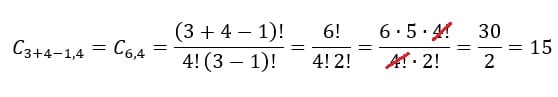
Combinação e arranjo
Podemos dizer que existe apenas uma única diferença entre combinação e arranjo. Em um arranjo, a ordem de escolha dos elementos importa e, em combinação, isso não ocorre.
Vídeos sobre combinação
Para que seus estudos fiquem ainda mais completos, serão apresentadas a seguir videoaulas sobre o assunto estudado até aqui. Acompanhe!
Combinação simples
Nesse vídeo, apresenta-se o conceito de combinação simples e, além disso, você confere também a sua fórmula.
Combinação com repetição
A combinação composta também não pode ficar de fora! Por isso, esse vídeo apresenta quais são os conceitos desse tipo de combinação, além de sua fórmula.
Exercícios resolvidos
Para que você se saia muito bem nas provas, essa videoaula traz exercícios resolvidos sobre o conteúdo. Confira!
Para fixar bem o conteúdo, é importante que você revise seus conhecimentos sobre análise combinatória, conjuntos e fatorial. E para continuar seus estudos de matemática, veja também nossa matéria sobre juros simples.
Referências
Matemática: ciência e aplicações (2010) – Iezzi et al.
Matemática: contexto & aplicações (2008) – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Combinação. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/combinacao. Acesso em: 01 de April de 2025.
1.
Em uma sala de aula, existem 12 alunas (uma delas chama-se Carla) e 8 alunos (um deles atende pelo nome de Luiz). Deseja-se formar comissões de 5 alunas e 4 alunos. Determine o número de comissões possíveis em que, simultaneamente, participem Carla e Luiz.
Comissão de alunas será dada por: C11,4
Comissão de alunos será composta por: C7,3
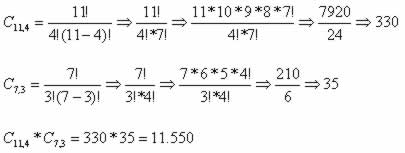
O número de comissões, respeitando a condição imposta, será 11550.
2.
Um pesquisador científico precisa escolher três cobaias em um grupo de oito cobaias. Determine o número de maneiras diferentes de se realizar essa escolha.
Temos a seguinte situação:
C8,3
Assim, substituindo na fórmula da combinação simples, temos:
![]()
O pesquisador pode realizar a escolha de 56 maneiras distintas.