Em muitas aplicações e transações financeiras, são utilzados os juros compostos, também chamados de juro sobre juro. Para conhecer a fórmula e saber como calcular, confira as informações e os exemplos a seguir. Veja também videoaulas e exercícios resolvidos para aprender bem o conteúdo!
Publicidade
Como calcular juros compostos?
O juro composto é conhecido também como juro sobre juro. Em outras palavras, o valor de juro gerado em um período é incorporado ao capital e passa a participar da composição de juro no período seguinte. Podemos calcular o juro composto da seguinte forma:
Relacionadas
- Capital (C): capital, ou seja, valor total a ser utilizado.
- Juros (J): valor total do juro.
- Taxa (i): taxa de juros, em porcentagem.
- Tempo (t): tempo em que será pago o produto ou o tempo de aplicação/transação financeira.
A fórmula do montante do juro composto é apresentada a seguir:
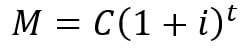
Agora que você já sabe o que é e como calcular esse tipo de juro, confira alguns exemplos de aplicação prática a seguir.
Publicidade
Exemplos de cálculo de juros compostos
De certa forma, ver apenas o conceito de algo acaba não sendo suficiente. Pensando nisso, serão apresentados, a seguir, alguns exemplos de aplicação do juro sobre juro. Acompanhe:
Problema que envolve o montante:
Mariana investiu R$800,00 à taxa de 0,8% ao mês, por três meses, no regime de juro composto. Qual será o montante de Mariana ao fim dessa aplicação?
Publicidade
Resolução

Problema que envolve o montante e o total de juros pago:
Um investidor aplicou R$500.000,00 a juro composto de 2% ao mês. Quantos reais ele terá após 5 meses de aplicação? Qual é o juro obtido?
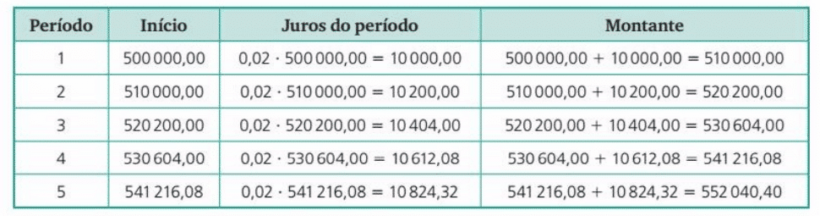
Resolução
Aqui, podemos utilizar a fórmula do montante para o juro composto. Dessa forma, teremos a seguinte situação:
M = 5000000*(1 – 0,02)5 = 552040,40
Então, o valor do montante final é de R$552.040,40. O juro total pode ser calculado com a fórmula J = M – C. Assim:
J = 552040,40 – 500000 = 52040,40
Portanto, o valor total dos juros é de R$52.040,40.
Saiba mais sobre juros compostos
Muitas são as dúvidas que temos quando estudamos. Para que suas questões possam ser sanadas, confira abaixo algumas videoaulas sobre o assunto estudado até aqui.
Um breve resumo sobre juros compostos
Nesse vídeo, é apresentada uma breve explicação sobre juros compostos, além de alguns exemplos de aplicação.
Mais exemplos
Aqui, você confere mais alguns exemplos de juros compostos para fixar bem o conceito!
Exercícios resolvidos
Para que você possa ir muito bem nas provas, aqui são apresentados alguns exercícios resolvidos sobre juros compostos. Acompanhe!
Por fim, é importante que você revise sobre os conteúdos de porcentagem, matemática financeira e juros simples. Bons estudos!
Referências
DANTE, Luiz Roberto. Matemática: contexto & aplicações. Ensino Médio.
IEZZI et al. Matemática: ciência e aplicações. Ensino Médio.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Juros compostos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/juros-compostos. Acesso em: 03 de April de 2025.
1.
Aplicando hoje na caderneta de poupança a quantia de R$ 20.000,00, qual será o montante gerado ao final de 4 anos, sabendo que a rentabilidade mensal é de 0,5%?
Temos os seguinte dados:
C= 20000
i = 0,5%a.m. = 0,005
n = 4 anos = 48 meses (observe que o tempo e a taxa devem estar no mesmo período)
Aplicando a fórmula:
M = 20000*(1+0,005)48
M = 20000*(1,005)48
M= 20000*1,2704891611
M = 25409,78
O montante gerado será de R$ 25409,78.
2.
Determinado capital gerou, após 24 meses, um montante de R$ 15.000,00. Sabendo que a taxa de juros é de 2% ao mês, determine o valor desse capital.
Temos os seguinte dados:
M = R$15000,00
C = ?
t = 24 meses
i = 2%a.m. = 0,02
Aplicando a fórmula do montante, temos:
15000 = C*(1 – 0,02)24
15000 = C * 1,6084372495
C = 15000/1,6084372495
C = 9325,82
Portanto, o capital era de R$ 9325,82.