A geometria plana é entendida na maioria das vezes como uma matéria da disciplina matemática básica, mas engloba, além disso, noções de algumas coisas mais complexas, como estatística, aritmética e álgebra, de forma que o estudo da geometria não pode ser feito de forma isolada. As figuras planas podem ser triânculos, quadrados, retângulos, ou ainda mais complexas, como o eneágono, decágono, icoságono, entre outros polígonos menos comuns, que são classificados de acordo com a quantidade de lados.
Publicidade
Como calcular o perímetro?
O perímetro pode ser calculado por meio da soma dos lados, em quaisquer figuras geométricas. Por exemplo, o quadrado tem quatro lados, e podemos representar o perímetro pela soma desses quatro lados: P= L’ + L’’ + L’’’ + L’’’’, ou ainda P = 4L, sendo P o perímetro e L os lados. A unidade de medida que devemos usar para o perímetro, é a mesma usada para mensurar os lados, uma vez que estamos realizando uma soma. Confira na imagem abaixo as fórmulas usadas para encontrar o perímetro de cada uma das principais figuras geométricas planas:
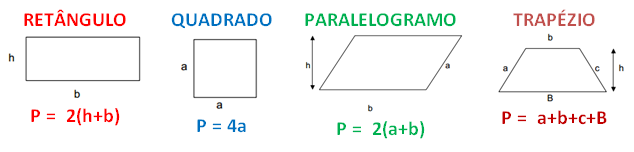
Como calcular a área?
O cálculo da área exige um pouco mais de conhecimento daquele que o realizará, já que diferentemente do perímetro, não se refere ao contorno da região, mas sim toda a superfície. Cada uma das figuras planas tem uma fórmula que permite que esse cálculo seja feito e, normalmente, nestas fórmulas, a área é representada pela letra S. A unidade de medida sempre será a unidade adotada por um lado elevada ao quadrado uma vez que trata-se de uma operação de multiplicação.
Fórmulas para cálculo da área
- Área do quadrado: S = l²
- Área do retângulo: S = b . h
- Área do triângulo: S = b . h / 2
- Losango: S = D . d / 2
Legenda:
- S = área
- l = lado
- b = base
- h = altura
- D = diagonal maior
- d = diagonal menor
Confira na imagem abaixo, algumas das fórmulas que podem ser usadas para calcular a área das figuras planas representadas (lembrando de conferir as letras usadas para representar elementos nas imagens).
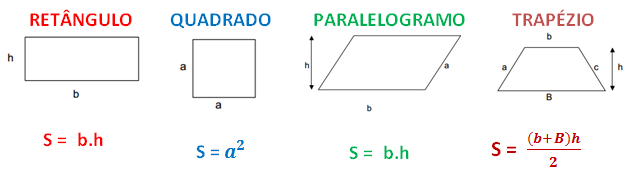
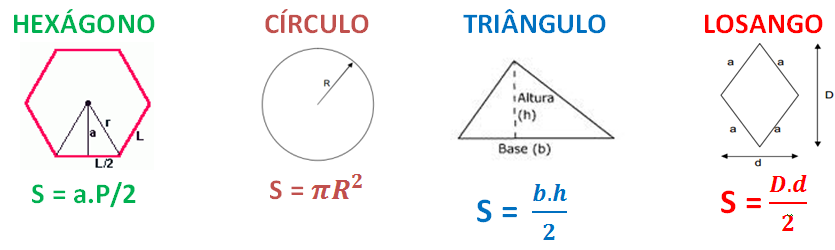
Círculo x Circunferência
No caso do círculo e da circunferência, é bastante comum encontrarmos problemas com relação à diferença entre eles e o cálculo para determinar a área e o perímetro. Quando estamos falando em circunferência, estamos nos referindo ao contorno e, portanto, ao comprimento, ao perímetro. Em contrapartida, quando falamos em círculo, estamos nos referindo à superfície e, portanto, à área.
O perímetro da circunferência pode ser encontrado por meio da fórmula: C = 2 π.r. A área do círculo, por sua vez, pode ser encontrada por meio da seguinte fórmula: Sc = π . r².
Onde C é circunferência, Sc é a área do círculo e r é o raio. Normalmente, para calcular, arredonda-se o valor de π para 3,14.
Publicidade
Referências
http://repositorio.furg.br/handle/1/1417
Coleção Matemática: Figuras e Formas – KS Smole, MI Diniz, P Cândido

Por Natália Petrin
Formada em Publicidade e Propaganda. Atualmente advogada com pós-graduação em Lei Geral de Proteção de Dados e Direito Processual Penal. Mestranda em Criminologia.
Petrin, Natália. Área e Perímetro. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/area-e-perimetro. Acesso em: 07 de January de 2026.
01. [ENEM] Em canteiros de obras de construção civil, é comum perceber trabalhadores realizando medidas de comprimento e de ângulos e fazendo demarcações por onde a obra deve começar ou se erguer. Em um desses canteiros foram feitas algumas marcas no chão plano. Foi possível perceber que, das seis estacas colocadas, três eram vértices de um triângulo retângulo e as outras três eram os pontos médios dos lados desse triângulo conforme pode ser visto na figura, em que as estacas foram indicadas por letras.
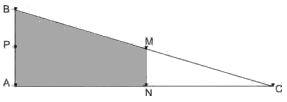
A região demarcada pelas estacas A, B, M e N deveria ser calçada com concreto. Nessas condições, a área a ser calçada corresponde
a) à mesma área do triângulo AMC.
b) à mesma área do triângulo BNC.
c) à metade da área formada pelo triângulo ABC.
d) ao dobro da área do triângulo MNC.
e) ao triplo da área do triângulo MNC.
02. [UFMT] Assinale a medida do lado de um quadrado, sabendo-se que o número que representa o seu perímetro é o mesmo que representa sua área.
a) 5
b) 4
c) 6
d) 8
01. [Para solucionar essa questão, devemos determinar a medida dos segmentos BP, PA, BM, MC, AN e NC. Essas medidas são estabelecidas por meio do ponto médio, que é o ponto que divide o segmento em duas partes iguais. Observe no desenho as medidas dos segmentos de acordo com os seus três pontos médios: M, N e P.
Agora que sabemos as medidas dos segmentos descritos anteriormente, podemos calcular a área.
Dados para o cálculo da área do triângulo MCN:
a = base
2
b = altura
2
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
AMCN = a . b
2 2
2
AMCN = ab . 1
4 2
AMCN = ab
8
8 . AMCN = ab
Dados para o cálculo da área do triângulo BAC:
a = base
b = altura
Fórmula para calcular a área do triângulo: A = base . altura
2
Cálculo da área do triângulo MCN:
ABAC = a . b
2
ABAC = 8 . AMCN
2
ABAC = 4 AMCN
ABAC = 3 AMCN + AMCN
Logo, AABMN = 3 AMCN
A área a ser calçada corresponde a 3 AMCN . Letra “e”.]
02. [Essa questão será resolvida pelo método de tentativas. Sendo assim, consideremos que o quadrado possui como medida de lado: 4, 5, 6 ou 8.
• O cálculo da área de um quadrado é dado pela seguinte fórmula: A = (lado)2 → A = l2.
• Já a fórmula do perímetro é a soma dos quatro lados do quadrado: P = l1 + l2 + l3 + l4
→ Considerando o lado do quadrado como 4, temos:
A = l2 → A = 42 → A = 16
P = l1 + l2 + l3 + l4 → P = 4 + 4 + 4 + 4 = 16
Quando o lado do quadrado é 4, a área é igual ao perímetro.
→ Considerando o lado do quadrado como 5:
A = l2 → A = 52 → A = 25
P = l1 + l2 + l3 + l4 → P = 5 + 5 + 5 + 5 = 20
Quando o lado do quadrado é 5, a área é diferente do perímetro.
→ Considerando o lado do quadrado como 6:
A = l2 → A = 62 → A = 36
P = l1 + l2 + l3 + l4 → P = 6 + 6 + 6 + 6 = 24
Quando o lado do quadrado é 6, a área é diferente do perímetro.
→ Considerando o lado do quadrado como 8:
A = l2 → A = 82 → A = 64
P = l + l + l + l → P = 8 + 8 + 8 + 8 = 32
Quando o lado do quadrado é 8, a área é diferente do perímetro.
Logo, a resposta para essa questão é a alternativa “b”.]