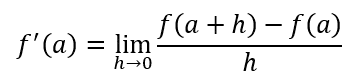Qual o intuito de aprender derivadas? A seguir, serão apresentados os motivos para se estudar esse conteúdo, além de informações sobre o que é a derivada de uma função, como surgiu o seu conceito e as principais regras de derivação. Confira para entender melhor!
Publicidade
O que é derivada de uma função?
De uma maneira geral, a derivada é a inclinação da reta tangente que passa por uma determinada curva. Além disso, é possível utilizar a derivada em física, pois ela também é uma taxa de variação, como na velocidade.
Relacionadas
De uma maneira mais formal, pode-se definir a derivada da seguinte maneira:
A derivada de uma função f em um número a, denotada por f'(a), é
se o limite existir.
Para entender esse conceito formal de derivada, é importante estudar e revisar sobre limites. Agora, que tal entender como surgiu o conceito de derivadas?
Como surgiu o conceito de derivadas?
O conceito de derivadas surgiu com Pierre Fermat no século XVII. Com seus estudos sobre funções, ele chegou a um empasse sobre a definição do que era uma reta tangente. Ele percebeu que algumas das funções estudadas não batiam com a definição de reta tangente da época. Isso ficou conhecido como “problema da tangente”.
Publicidade
Foi então que ele resolveu o problema da seguinte maneira: para determinar uma reta tangente a uma curva no ponto P, ele definiu um outro ponto Q na curva e considerou a reta PQ. Dessa forma, aproximou o ponto Q ao ponto P, obtendo assim retas PQ que se aproximavam de uma reta t, que Fermat chamou de reta tangente ao ponto P.
Essas foram as ideias consideradas como “embriões” para o conceito de derivadas. Entretanto, Fermat não possuía as ferramentas necessárias – por exemplo, o conceito de limite, por ainda não ser conhecido na época. Foi apenas com Leibniz e Newton que o cálculo diferencial tornou-se possível e importante para as ciências exatas.
Regras de derivação
Para facilitar o cálculo de derivadas, algumas regras de derivação foram “criadas”. Dessa forma, vamos conhecer algumas dessas regras. Vamos considerar que f(x) e g(x) são funções genéricas que dependem da variável x, e f'(x) e g'(x) são as derivadas dessas funções, respectivamente.
Publicidade
Regra da potência
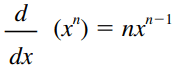
Essa regra é conhecida como regra do “tombo”. Isso se deve ao fato de que a potência n “cai” quando derivamos uma função potência. Por exemplo, a derivada de f(x) = x2 é f'(x) = 2x.
Regra da multiplicação por constante

O que acontece aqui é que a derivada de uma constante vezes uma função é a constante vezes a derivada da função. Em outras palavras, a constante “sai” e fazemos apenas a derivada da função. Por exemplo, vamos considerar a função f(x) = 3x4. Sua derivada é:

Regra da soma

A derivada de uma soma de duas funções f(x) e g(x) é a soma das derivadas de f(x) e g(x). Por exemplo, seja h(x) = 3x + 5x². A derivada de h(x) é h'(x) = 3 + 10x.
Regra da diferença
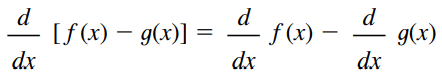
Essa regra segue a mesma ideia da regra anterior, porém ela se refere à diferença entre duas funções. Em outras palavras, a derivada da diferença entre f(x) e g(x) é a diferença entre as derivadas de f(x) e g(x).
Derivada da função exponencial natural
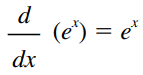
A derivada da função exponencial f(x) = ex é ela mesma.
Regra do produto
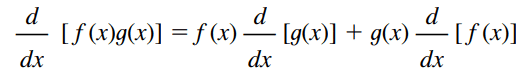
Em outras palavras, a regra do produto diz que a derivada de um produto de duas funções é a primeira função vezes a derivada da segunda função mais a segunda função vezes a derivada da primeira função.
Regra do quociente
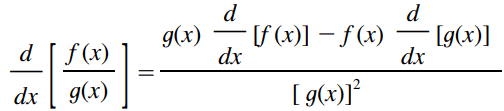
Ou seja, a derivada de um quociente é o denominador vezes a derivada do numerador menos o numerador vezes a derivada do denominador, todos divididos pelo quadrado do denominador.
Essas são algumas das regras de derivação. Existem muitas outras, como a regra de derivação para funções trigonométricas, entre outras.
Saiba mais sobre derivadas
Para que você tenha um melhor entendimento sobre o assunto estudado, serão apresentadas, a seguir, algumas videoaulas. Bons estudos!
Derivadas: definição e cálculo
Aqui, você entenderá um pouco mais sobre o conceito de derivada e como realizar o seu cálculo a partir da definição dela.
Principais regras de derivação
Nesse vídeo, são apresentadas algumas das regras de derivação e como aplicá-las. Acompanhe!
Exercícios resolvidos
Para que você entenda melhor sobre as regras de derivação, apresentamos aqui um vídeo com alguns exercícios resolvidos. Confira!
Por fim, a derivada é de extrema importância na matemática, física, química e biologia. Esse assunto também é pertinente para outras áreas, como economia, ciências contábeis, entre outras. Não deixe de estudar também sobre funções para se aprofundar nos seus estudos!
Referências
Cálculo: volume 1 (2006) – James Stewart

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Derivadas. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/derivadas. Acesso em: 03 de April de 2025.
1.
Calcule a derivada das funções abaixo:
a) f(x) = x²
b) f(x) = 20
c) f(x) = 5x³ + 2x
d) f(x) = x³ + 1000
e) f(x) = x³ + x² + x + 1
a) Utilizando a regra da potência: f'(x) = 2x
b) A derivada de uma constante é zero
c) Utilizando a regra da potência e a regra da soma, obtém-se a resposta: f'(x) = 3.5x² + 2 = 15x² + 2
d) Utilizando a regra da potência, derivada de uma constante e a regra da soma, obtém-se a resposta: f'(x) = 3x²
e) Utilizando a regra da potência e a regra da soma, obtém-se a resposta:
f'(x) = 3x² + 2x + 1
2.
Encontre a inclinação da reta tangente, no ponto x=1, a seguinte curva:
![]()
Sabemos que a inclinação da reta tangente em um ponto é a derivada da função naquele ponto, portanto:
m = f'(1)
Vamos então calcular a derivada de f(x), utilizando a regra da soma e da potência. Assim:
f'(x) = 110x10 – 50x9 + 28x3 + 3x2
Dessa forma, vamos calcular agora a derivada no ponto x = 1. Assim:
f'(1) = 110 – 50 + 28 + 3 = 91
Portanto, a inclinação da reta tangente à curva é:
m = 91