Como o próprio nome sugere, o plano inclinado é uma superfície plana na qual os pontos inicial e final estão em alturas diferentes. A força necessária para carregar um objeto entre o início e o fim da trajetória citada é menor no plano inclinado do que em uma trajetória completamente vertical.
Publicidade
O que é plano inclinado?
Relacionadas
Plano inclinado pode ser entendido como um tipo de máquina simples. Ele está muito presente em nosso cotidiano. Por exemplo: é mais difícil subir um lance de escadas do que fazer o mesmo trajeto por meio de uma rampa. Para vencer cada degrau, precisamos realizar uma força maior que o peso do nosso corpo. Já para subir uma rampa, realizamos uma força maior que um dos componentes do peso.
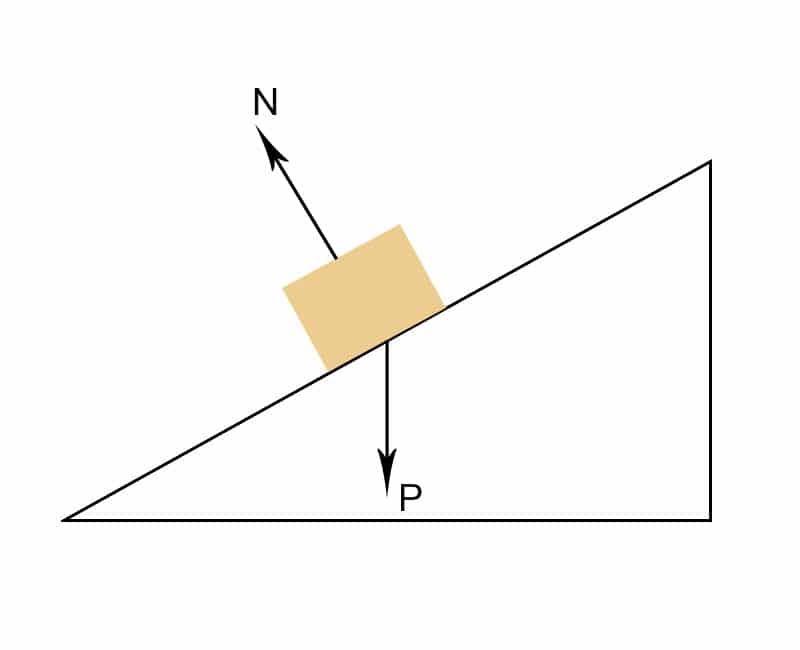
Observe na figura que, neste caso, a força normal e a força peso não têm a mesma direção. Isso acontece porque a força normal é sempre perpendicular à superfície na qual o corpo se encontra. Logo, se o objeto está em uma superfície inclinada, a força normal estará a 90° do plano. Já a força peso sempre aponta para baixo.
Tipos de plano inclinado
Para o estudo do plano inclinado, devemos decompor a força peso em componentes x e y, isto é, em componentes horizontais e verticais respectivamente. Consideramos como componente horizontal a superfície do plano inclinado e componente vertical é perpendicular a ela. Dessa forma, as forças que estão sobre a superfície do plano estão na horizontal. Seguindo este raciocínio, podemos realizar o cálculo para diferentes tipos de plano inclinado:
Plano inclinado sem atrito
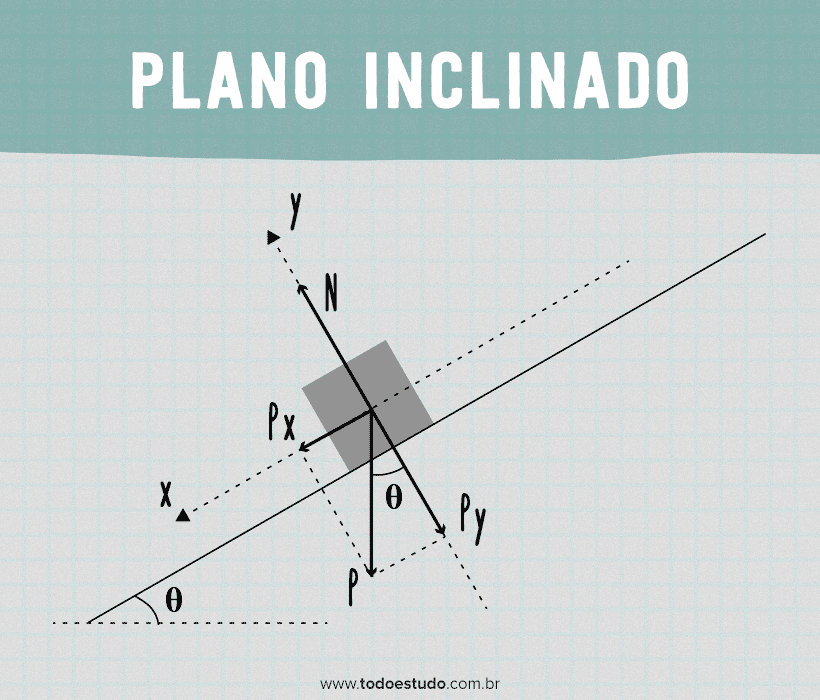
No plano inclinado sem atrito, escrevemos as forças que atuam sobre o bloco. Além disso, decompomos a força peso em componentes verticais e horizontais. A componente vertical do peso (Py) será oposta à força normal. Já o seu componente horizontal (Px) será a força responsável pelo movimento. Assim, devemos encontrar a força resultante para a vertical (y) e horizontal (x). Desta forma:
Publicidade
Na vertical, isto é, a força em y:
Fy = N – Py = 0
Em que,
Publicidade
- Fy: Componente vertical da força resultante (N);
- N: Força normal (N);
- Py: Componente vertical do peso (N);
Como não há movimento vertical, ou seja, como o objeto não “pula” no plano inclinado, a força resultante na vertical é nula. Concluímos que:
N = Py
Porém, sabemos que a força peso é dada pelo produto da massa pela aceleração gravitacional. Além disso, como estamos lidando com um componente desta força, consideramos a projeção do vetor do peso sobre o eixo y. Assim:
N = mg cosθ
Em que,
- N: Força normal (N);
- m: Massa do bloco (kg);
- g: Aceleração da gravidade (m/s2);
- cosθ: Cosseno do ângulo de inclinação do plano;
Já para o componente horizontal, isto é, a força em x, temos:
Fx = Px = m a
Em que,
- Fx: Componente horizontal da força resultante (N);
- Px: Componente horizontal do peso (N);
- m: Massa do bloco (kg);
- a: Aceleração a(m/s2);
Novamente, o peso é dado pelo produto da massa pela aceleração da gravidade no local. Porém, agora consideramos a projeção do vetor peso sobre o eixo x. Assim:
Px = mg senθ
Em que,
- Px: Componente horizontal do peso (N);
- m: Massa do bloco (kg);
- g: Aceleração da gravidade (m/s2);
- senθ: Seno do ângulo de inclinação do plano;
Note que a única força horizontal que atua sobre o bloco é o componente horizontal do peso. Isso acontece porque não há atrito entre o corpo e a superfície do plano inclinado. Vejamos agora o que acontece se houver atrito:
Plano inclinado com atrito
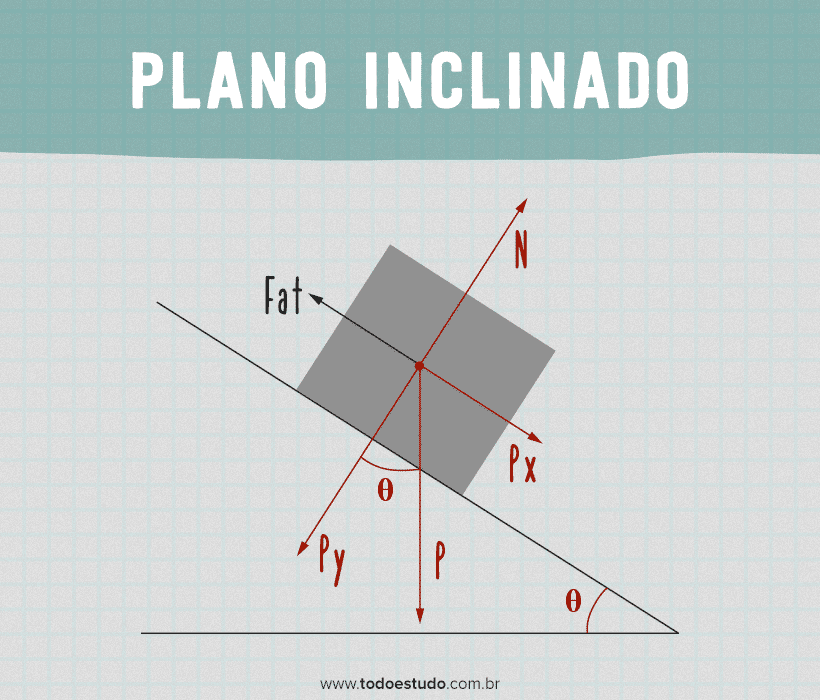
Caso haja atrito entre o corpo e a superfície do plano inclinado, a força de atrito estará no sentido oposto da componente horizontal da força peso. Além disso, no componente vertical, o cálculo da força continua igual ao cálculo do plano inclinado sem atrito.
Desta forma, para o componente vertical, temos:
Fy = N – Py = 0
Em que,
- Fy: Componente vertical da força resultante (N);
- N: Força normal (N);
- Py: Componente vertical do peso (N);
Como não há movimento vertical, ou seja, como o objeto não “pula” no plano inclinado, a força resultante na vertical é nula. Concluímos que:
N = mg cosθ
Em que,
- N: Força normal (N);
- m: Massa do bloco (kg);
- g: Aceleração da gravidade (m/s2);
- cosθ: Cosseno do ângulo de inclinação do plano;
Já para o componente horizontal, consideramos a força de atrito a qual é dada por
Fat = ?N
Em que,
- Fat: Força de atrito (N);
- ?: Coeficiente de atrito (essa grandeza física não possui unidade de medida);
- N: Força normal (N);
Assim, a força resultante na horizontal será:
Fx = Px – Fat = m a
Em que,
- Fx: Componente horizontal da força resultante (N);
- Fat: Força de atrito (N);
- Px: Componente horizontal do peso (N);
- m: Massa do bloco (kg);
- a: Aceleração a(m/s2);
Caso o corpo esteja em repouso em relação ao plano ou com velocidade constante, teremos:
Fx = Px – Fat = 0
Px = Fat
Em que,
- Fx: Componente horizontal da força resultante (N);
- Fat: Força de atrito (N);
- Px: Componente horizontal do peso (N);
Caso o corpo esteja parado sobre a superfície inclinada, note que consideramos o atrito estático. Se houver movimento, consideramos o atrito dinâmico. Além disso, o componente horizontal do será igual à força de atrito apenas se o bloco estiver em repouso ou se estiver se deslocando com velocidade constante.
Caso o corpo estiver desenvolvendo um movimento uniformemente variado, isto é, com aceleração constante, deve-se considerar a seguinte relação:
Fx = Px – Fat = m a
Em que,
- Fx: Componente horizontal da força resultante (N);
- Fat: Força de atrito (N);
- Px: Componente horizontal do peso (N);
- m: Massa do bloco (kg);
- a: Aceleração a(m/s2);
Além da possibilidade do cálculo das força envolvidas no plano, podemos calcular a aceleração em ambos os casos.
Aceleração no plano inclinado
A aceleração do plano inclinado dependerá do ângulo de inclinação e, também, da aceleração da gravidade no local. No plano sem atrito, encontramos anteriormente que a força resultante na horizontal será igual ao componente x do peso. Isto é:
Fx = Px
Em que,
- Fx: Força resultante horizontal do peso (N);
- Px: Componente horizontal do peso (N);
Além disso, sabemos que a força resultante é o produto da massa pela aceleração do corpo e a força peso em x é o produto da massa, da aceleração da gravidade no local e do seno do ângulo de inclinação. Assim:
ma =mg senθ
Em que,
- m: Massa do corpo (kg);
- a: Aceleração (m/s2);
- g: Aceleração da gravidade (m/s2);
- senθ: Seno do ângulo de inclinação do plano.
Como há massa em ambos os lados da igualdade, podemos tirá-la da equação. Desta forma, ficamos com:
a =g senθ
Em que,
- a: Aceleração (m/s2);
- g: Aceleração da gravidade (m/s2);
- senθ: Seno do ângulo de inclinação do plano.
Note que a aceleração no plano inclinado não dependerá da massa do corpo, apenas da aceleração da gravidade no local e da inclinação do plano. É possível ver que a aceleração do corpo será igual a aceleração gravitacional em um caso limite de um plano com inclinação igual a 90°, porque sen (90°) = 1.
Videoaulas sobre plano inclinado
Agora que já aprendemos sobre o plano inclinado, sua teoria e seus cálculos, vamos aprofundar nosso conhecimento.
Experimento sobre o plano inclinado
Veja uma demonstração experimental do plano inclinado.
Plano inclinado sem atrito
Agora, observe os princípios do plano inclinado sem atrito.
Plano inclinado com atrito
Aprofunde seus conhecimentos sobre o plano inclinado com atrito.
Este assunto muito comum tanto em nosso cotidiano, quanto em avaliações de física. Além disso, é possível relacionar e observar que os cálculos utilizados são aplicações diretas da segunda lei de Newton sobre aceleração e dos conceitos de estática. Vale a pena conferir!
Referências
MENEZES, L. C. et al. Leituras de Física (GREF): Mecânica – ler, pensar e fazer. São Paulo: Instituto de Física da USP. 1998.

Por Hugo Shigueo Tanaka
Divulgador Científico e co-fundador do canal do YouTube Ciência em Si. Historiador da Ciência. Professor de Física e Matemática. Licenciado em Física pela Universidade Estadual de Maringá (UEM). Mestre em Ensino de Ciências e Matemática (PCM-UEM). Doutorando em Ensino de Ciências e Matemática (PCM-UEM).
Tanaka, Hugo Shigueo. Plano inclinado. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/plano-inclinado. Acesso em: 01 de January de 2026.
1. [UECE]
Suponha que uma esfera de aço desce deslizando, sem atrito, um plano inclinado. Pode-se afirmar corretamente que, em relação ao movimento da esfera, sua aceleração
a)aumenta e sua velocidade diminui.
b)e velocidade aumentam.
c)é constante e sua velocidade aumenta.
d)e velocidade permanecem constantes
Pelos estudos do plano inclinado vistos anteriormente, temos que:
a = g sen θ
Dessa forma, como a aceleração depende apenas da aceleração gravitacional e da inclinação do plano, as quais são constantes, a bolinha desenvolve um Movimento Uniformemente Variado (MUV).
Logo, a aceleração é constante e a velocidade aumenta de maneira linear.
Resposta correta: C.
2. [UEG - Adaptada]
Sobre um plano inclinado e colocada uma caixa em repouso e fixada a um cabo inextensível de massa desprezível. Não existe atrito entre a caixa e o plano inclinado.
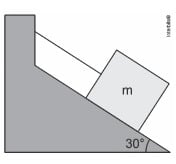
Qual será a aceleração da caixa ao se cortar o cabo?
Analisando as forças que atuam sobre o bloco:
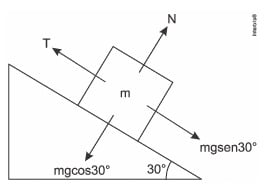
Nesse caso, a força de tração (T) é igual ao peso do corpo em x (mg sen30°).
Ao cortar o cabo, temos que a aceleração desenvolvida pelo corpo será igual a aceleração da gravidade vezes o seno de 30 graus:
a = g sen 30°
O exercício não fornece valores para as acelerações. Porém, podemos substituir o valor de sen 30°, que é 1/2.
Assim:
a = g/2
Ou seja, a aceleração desenvolvida pela caixa é igual a metade da aceleração gravitacional.