Polígonos

Na Geometria Plana ou Euclidiana, um polígono (do grego poli = muitos, gono = ângulos) é uma superfície plana limitada por uma linha poligonal fechada.

Publicidade

A linha poligonal é uma linha formada apenas por segmentos de reta. As figuras fechadas denominadas polígonos são caracterizadas pela presença de ângulos, vértices, diagonais e lados.

Nome dos polígonos

Os polígonos recebem denominações especiais de acordo com o número n de lados. Confira a seguir:

• 3 lados: triângulo ou trilátero;
• 4 lados: quadrângulo ou quadrilátero;
• 5 lados: pentágono;
• 6 lados: hexágono;
• 7 lados: heptágono;
• 8 lados: octógono;
• 9 lados: eneágono;
• 10 lados: decágono;
• 11 lados: undecágono;
• 12 lados: dodecágono;
• 15 lados: pentadecágono;
• 20 lados: icoságono.

“Em geral, para um número n (n ≥ 3) qualquer de lados dizemos que o polígono é um: n-látero.” (DOLCE e POMPEO, 1997, p. 135)

Os elementos de um polígono

Dentre os elementos de um polígono estão os vértices, lados, ângulos, lados e ângulos consecutivos e não consecutivos e perímetro.

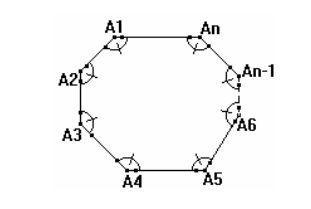
Considerando o polígono acima, temos que:

Publicidade

• Vértices: Os pontos A1, A2, A3, A4 etc
• Lados: Os segmentos A1-A2, A2-A3, A3-A4 etc
• Lados consecutivos: Dois lados que têm um vértice comum (ou uma extremidade comum);
• Lados não-consecutivos: Não têm vértice (ou extremidade) comum;
• Ângulos consecutivos: Dois ângulos são consecutivos se apresentam um lado do polígono comum;
• Perímetro: É a soma dos lados.

Polígonos convexos e não convexos

“Um polígono simples é um polígono convexo se, e somente se, a reta determinada por dois vértices consecutivos quaisquer deixa todos os demais (n – 2) vértices num mesmo semiplano dos dois que ela determina.” (DOLCE e POMPEO, 1997, p. 134)

Caso os ângulos sejam menores do que 180º, o polígono será convexo.

Se um polígono não é convexo, ele é um polígono côncavo, e apresenta um ângulo maior do que 180º.

Publicidade

Os ângulos de um polígono

A soma dos ângulos internos de um polígono depende do número de lados (n). O cálculo é feito pela seguinte expressão:

S = (n – 2) . 180º, onde S = a soma dos ângulos internos; n = número de lados.

Cada ângulo externo do polígono é o suplemento do respectivo ângulo interno. A soma dos ângulos externos de um polígono é dada pela seguinte expressão:

Se = 360º.

Polígono regular e irregular

• Polígonos regulares: possuem todos os lados e ângulos com medidas iguais.



• Polígonos irregulares: não possuem ângulos nem lados com medidas iguais.

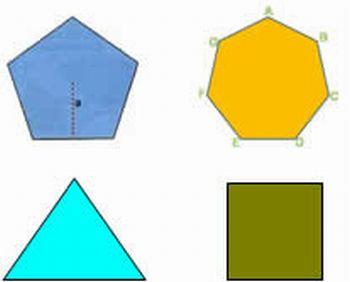
As diagonais de um polígono

A diagonal de um polígono é qualquer segmento de reta que une dois vértices não consecutivos. O número de diagonais de um polígono depende do número de lados (n) e é dado pela seguinte expressão:

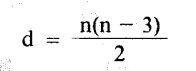
Referências