“Isaac Newton nasceu no interior da Inglaterra, tendo estudado no Trinity College em Cambridge. (…) Por ocasião da peste, voltou para casa pois o colégio foi fechado e neste período fez suas principais descobertas: o teorema binomial, o cálculo, a lei da gravitação e a natureza das cores.” (Hazzam, 2004, pg. 46-E).
Publicidade
O nome é uma homenagem ao físico e matemático inglês Isaac Newton, que estabeleceu regras que valem para (a+b)n quando o expoente n é fracionário ou inteiro negativo. A partir desses estudos de Newton foi desenvolvido o método que possibilita desenvolver a enésima potência de um binômio, conhecido como Binômio de Newton, representado pela seguinte fórmula:
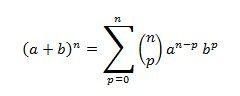
Portanto, denomina-se Binômio de Newton, a todo binômio da forma (a + b)n, sendo n um número natural, que é chamado de ordem do binômio. O desenvolvimento de um binômio onde n > 3 é baseado num conjunto de regras. Para valores de n entre 2 e 3, utiliza-se o conceito de produtos notáveis, aplicando a propriedade distributiva. Portanto, o Binômio de Newton é considerado um complemento do estudo de Produtos Notáveis.
Para desenvolver o Binômio de Newton é preciso entender os conceitos de Coeficientes Binomiais e o Triângulo de Pascal. O número de termos resultantes do desenvolvimento do binômio será sempre n+1.
Coeficientes Binomiais
O coeficiente binomial, de um número n, na classe k, consiste no número de combinações de n termos, k a k, representado pela seguinte equação:
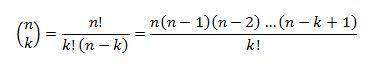
Publicidade
Triângulo de Pascal
Já o Triângulo de Pascal é um triângulo aritmético formado por números que têm diversas relações entre si. Muitas dessas relações foram descobertas pelo próprio Pascal, físico e matemático francês do século XVII.
A fórmula matemática para construir o Triângulo de Pascal determina que cada linha terá um número a mais que a anterior. Assim, toda linha n possui n+1 elementos, sempre aplicando a primeira linha como sendo a linha 0. Em cada elemento , é determinado que n é o número da linha e k o número da coluna.
Para construir as linhas do triângulo, a propriedade denominada Relação de Stifel estabelece que qualquer número terá valor igual a soma dos dois números que se encontram na linha acima, somados a partir do número 1 da extremidade.
Publicidade
Exemplo:
1
1 1
(1 + 2) 1
1 (3) 3 1
1 4 (6 + 4) 1
1 5 10 (10) 5 1
Para cada linha do triângulo, é associado um número:
Linha 0: 1
Linha 1: 1 1
Linha 2: 1 2 1
Linha 3: 1 3 3 1
Linha 4: 1 4 6 4 1
Linha 5: 1 5 10 10 5 1
Linha 6: 1 6 15 20 15 6 1
A soma dos números em determinada linha n, se dá pelo resultado da expressão 2n. Logo, para a linha 4 a soma dos número que a compõe é 24=16, ou seja, 1+4+6+4+1=16. A sequência de números apresentada na linha 4 é a mesma sequência de números binomiais que será encontrada quando desenvolvemos a equação.
Exemplo:
(2x+1)4=)* 2x4*10+ )* 2x3*11+)* 2x2*12+)* 2x1*13+)* 2x0*14
Obetemos então a expressão:
1.16×4.1 + 4.8×3.1 + 6.4×2.1 + 4.2x . 1 + 1.1.1
Existe uma forma simplificada para obter a soma dos coeficientes numérico do desenvolvimento de um binômio:
– troque qualquer letra do binômio por 1
– calcule o valor que ficará dentro dos parênteses
No desenvolvimento do bin6omio acima, a soma dos coeficientes é 81 (16 + 32 + 24 + 8 + 1)
1.16x4.1 + 32x3.1 + 24x2.1 + 8x . 1 + 1
Utilizando a dica dada:
(2x+1)4
(2.1 + 1)4 = 34 = 81
Você Sabia?
Aplicações do Binômio de Newton
Umas das áreas em que o Binômio de Newton é utilizado é na genética. No caso de herança quantitativa, ou poligênica, onde participam dois ou mais pares de genes. A interação que ocorre entre os genes (poligenes) que transmitem as características herdadas, acontece de tal forma que cada um deles é responsável por uma parcela do fenótipo resultante. O padrão de distribuição de herança, nesse caso, segue o padrão do Binômio de Newton, sendo (p + q)n, onde n é o número de poligenes. Entre os exemplos de herança quantitativa temos características como cor de pele, cor do olho humano, altura, peso e cor do cabelo.
Referências
HAZZAN, S. Fundamentos da Matemática Elementar. Combinatória e Probabilidade. Volume 5. 3 Edição. São Paulo: Atual Editora, 2004.
LOPES, S. Bio- Volume Único. 1ª Edição, 3ª Triagem. São Paulo: Editora Saraiva, 2005.

Por Carlos Ferreira
Formado em Ciências Econômicas e Jornalismo. Possui ampla experiência editorial e redacional em conteúdos jornalísticos com foco em mídias digitais.
Ferreira, Carlos. Binômio de Newton. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/binomio-de-newton. Acesso em: 18 de December de 2025.
1. (FGV/2013) Desenvolvendo-se o binômio P(x) = (x + 1)5 , podemos dizer que a soma de seus coeficientes é:
a) 16
b) 24
c) 32
d) 40
e) 48
(UEM/2013) A soma dos algarismos do termo independente de x no desenvolvimento do binômio de Newton é:
a) 3
b) 4
c) 6
d) 7
1. [c]
A soma dos coeficientes é: P (1) = (1 + 1)5 = 25 = 32
2. [b]
![]()
O termo independente de x é o natural p que torna o expoente de x igual a zero, ou seja,
2p-8=0, logo p=4
Substituindo:
![]()