A teoria dos conjuntos é muito importante não só para a matemática, mas também para outras matérias, pois permite agrupar determinado tipo de informações. Essa teoria foi formulada por Georg Cantor em 1874, com uma publicação no Jornal de Crelle. A seguir, confira notação, símbolos e operações de conjuntos numéricos, além de videoaulas e exercícios resolvidos sobre o tema.
Publicidade
Notação e representação de conjuntos
Antes de mais nada, um conjunto pode ser definido como uma coleção de objetos chamados elementos. Esses elementos são agrupados conforme uma propriedade comum entre eles ou que satisfaz a uma determinada condição.
Relacionadas
Logo, é possível representar um conjunto de várias maneiras. Geralmente, os conjuntos são representados por letras maiúsculas e os seus elementos, por letras minúsculas, no caso em que não são numerais. Veja abaixo cada um dessas maneiras de representação.
Representação por chaves com separação entre vírgulas: “{ }”
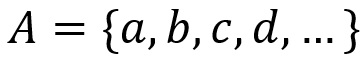
Nessa representação, os elementos são colocados entre chaves, sendo separados por vírgulas. A vírgula também pode ser trocada por ponto e vírgula (;).
Representação por propriedades dos elementos
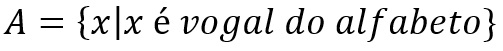
Publicidade
Outra representação possível é a partir das propriedades do elemento. Por exemplo, na imagem acima, o conjunto será composto apenas pelas vogais do alfabeto. Essa forma de demonstrar um conjunto é utilizada para conjuntos que possam vir a ocupar muito espaço.
Representação por diagrama de Venn
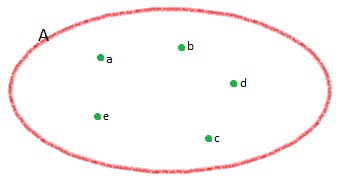
Esse esquema é muito utilizado quando se trata de funções de um modo geral. Além disso, essa representação é conhecida como diagrama de Venn.
Publicidade
Cada representação pode ser utilizada em diferentes situações, dependendo apenas de qual é a mais apropriada para ser usada no caso.
Símbolos dos conjuntos
Além das representações, existem também os símbolos dos conjuntos. Esses símbolos são utilizados para definir se um elemento pertence ou não a um determinado conjunto, por exemplo, entre vários outros significados e símbolos. A seguir, confira alguns elementos dessa simbologia de conjuntos:
- Pertence (∈): quando um elemento pertence a um conjunto, utiliza-se o símbolo ∈ (pertence) para representar tal situação. Por exemplo, i∈A é lido como i pertence ao conjunto A.
- Não pertence (∉): representa o contrário do símbolo anterior, ou seja, serve para quando um elemento não pertence a um determinado conjunto.
- Símbolo de contido (⊂) e contém (⊃): se o conjunto A é subconjunto do conjunto B, dizemos que A está contido em B (A ⊂ B) ou, ainda, que B contém A (B ⊃ A).
Esses são alguns dos símbolos mais utilizados para os conjuntos. Continue a leitura para aprender mais sobre o assunto!
Conjuntos numéricos usuais
Conforme a humanidade foi evoluindo, juntamente com a matemática, a necessidade de contar as coisas e organizá-las melhor foi se fazendo presente no cotidiano. Dessa forma, surgiram os conjuntos numéricos, uma forma de diferenciar os tipos de numerais existentes conhecidos até hoje. Neste tópico, você vai aprender sobre os conjuntos dos números naturais, inteiros e racionais.
Números naturais
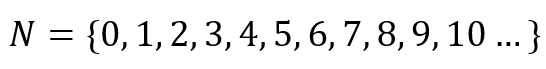
A partir de zero e sempre acrescentando uma unidade, obtém-se o conjunto dos números naturais. Além disso, esse conjunto é infinito, ou seja, ele não possui um “tamanho” bem definido.
Números inteiros
![]()
Utilizando os símbolos de + e –, para todos os números naturais, é possível determinar o conjunto dos números inteiros. Assim, obtém-se um número positivo e outro negativo.
Números racionais
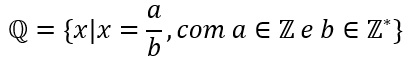
Quando se tenta dividir, por exemplo, 1 por 3 (1/3), obtém-se um resultado sem solução no conjunto dos números naturais ou inteiros – ou seja, o valor não é exato. Houve então a necessidade de se determinar um outro conjunto conhecido como conjunto dos números racionais.
Além desses, existem também os conjuntos dos números irracionais, reais e imaginários, com características mais complexas.
Operações com conjuntos
É possível realizar operações com os conjuntos, que auxiliam nas aplicações dos mesmos. Entenda mais sobre cada uma a seguir:
União de conjuntos
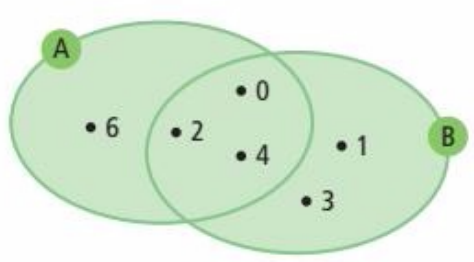
Um conjunto é formado por todos os elementos de A ou B, de modo que ocorre uma união entre os dois conjuntos (A ∪ B).
Intersecção de conjuntos
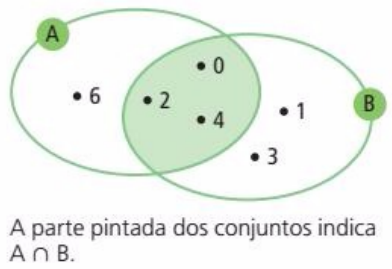
Por outro lado, para um conjunto formado pelos elementos que estão, ao mesmo tempo, em A e em B, diz-se que esse conjunto forma uma intersecção entre os outros dois. Ou seja, tem-se que A ∩ B.
Número de elementos da união de conjuntos
É possível saber qual é o número de elementos da união de um conjunto A com um conjunto B. Para isso, utiliza-se a seguinte relação:
![]()
Tome como exemplo os conjuntos A={0,2,4,6} e B={0,1,2,3,4}. O primeiro conjunto contém 4 elementos e o segundo possui 5 elementos. Porém, quando se faz a união deles, o número de elementos de A ∩ B é contado duas vezes, por isso subtrai-se n(A ∩ B).
Essas operações são importantes para o desenvolvimento de alguns exercícios e para um maior entendimento sobre os conjuntos.
Videoaulas para entender mais sobre conjuntos
Até aqui, você viu algumas definições e operações dos conjuntos. Dessa forma, que tal entender um pouco mais sobre esse conteúdo com o auxílio dos vídeos abaixo? Acompanhe as explicações!
Conceitos introdutórios
Com o vídeo acima, é possível ter um pouco mais de conhecimento sobre os conceitos introdutórios da teoria de conjuntos. Além disso, você poderá entender tal teoria através de exemplos.
Exercício resolvido com diagrama de Venn
É possível resolver exercícios de conjuntos utilizando o diagrama de Venn, como mostra o vídeo acima. Confira para entender melhor!
Conjuntos numéricos
Já nesse vídeo, é possível entender um pouco mais sobre os conjuntos numéricos e algumas de suas propriedades. Veja na íntegra!
Como você viu, a teoria dos conjuntos está presente no cotidiano. A partir dela, é possível agrupar muitas coisas em um conjunto para facilitar a vida e o dia a dia.
Referências
Matemática completa 1 – José Roberto Bonjorno
Matemática: contexto e aplicações – Luiz Roberto Dante

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Conjuntos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/conjuntos. Acesso em: 02 de April de 2025.
1. [Unifap]
O dono de um canil vacinou todos os seus cães, sendo que 80% contra parvovirose e 60% contra cinomose. Determine o porcentual de animais que foram vacinados contra as duas doenças.
Podemos representar essa situação pelo diagrama de Venn a seguir:
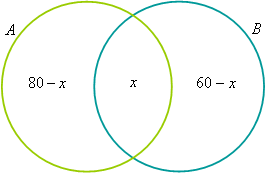
Sabemos que a soma de todos os percentuais que são mostrados acima é 100%. Assim, temos que:
80 – x + x + 60 – x = 100
140 – 2x + x = 100
– x = 100 – 140
– x = – 40
x = 40
RESPOSTA: 40%
2. [UFSE]
Os senhores A, B e C concorriam à liderança de certo partido político. Para escolher o líder, cada eleitor votou apenas em dois candidatos de sua preferência. Houve 100 votos para A e B, 80 votos para B e C e 20 votos para A e C. Em consequência:
a) venceu A, com 120 votos.
b) venceu A, com 140 votos.
c) A e B empataram em primeiro lugar.
d) venceu B, com 140 votos.
e) venceu B, com 180 votos.
Como cada eleitor podia votar em apenas dois candidatos, precisamos olhar o total de votos das intersecções de A e B, A e C e B e C, conforme a figura a seguir:
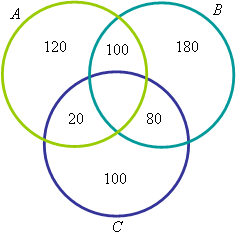
Assim, temos que:
Votos recebidos pelo candidato A = 100 + 20 = 120
Votos recebidos pelo candidato B = 100 + 80 = 180
Votos recebidos pelo candidato C = 80 + 20 = 100
Portanto, o candidato B ganhou a eleição, com 180 votos.
RESPOSTA: e)