Os primeiros termômetros precisos de líquido em vidro foram construídos por volta do ano de 1717 por um fabricante de instrumentos, o físico e engenheiro alemão Daniel Gabriel Fahrenheit (1686-1736). Seu termômetro trazia mercúrio em um bulbo de vidro, tendo representado um grande avanço tecnológico para a época – sobretudo em razão da dificuldade para a fabricação de capilares finos com diâmetro perfeitamente uniforme.
Publicidade
Na termometria prática existe o problema de criar uma escala de temperatura que sempre possa ser produzida, de tal forma que, se fizéssemos medidas de temperatura, por exemplo, do ponto de fusão da água em Maringá às 8 horas do dia 25 de Dezembro de 2015 e em Oslo (Noruega) às 14 horas do dia 27 de Dezembro, o resultado, ao ser comparado, não pode trazer dúvida sobre o fenômeno e nem sobre escala de temperatura (lógico que sobre as mesmas condições de pressão).

Fahrenheit usou um processo eminentemente empírico para criar uma escala para o seu termômetro. Ao aperfeiçoar a escala termométrica de Roemer (1644 – 1710), ele graduou seu instrumento definindo como zero de temperatura a mais baixa atingida por ele em seu laboratório, que era a temperatura de uma mistura de gelo e sal, mergulhando o bulbo na mistura e fez uma marcação na sua escala. Para definir a temperatura superior, que decidiu chamar de 100°, considerou a temperatura normal do corpo humano.
Logo, um grau Fahrenheit é 1/100 da diferença de temperatura entre duas temperaturas limite, que são chamadas de pontos fixos. Porém, esses fenômenos utilizados por Fahrenheit para definir tais pontos se mostraram não reprodutíveis com precisão. Por exemplo, com a mistura de gelo e sal, podemos obter como temperatura mais baixa 6 graus Fahrenheit, que seria mais baixa do que a conseguida por ele.
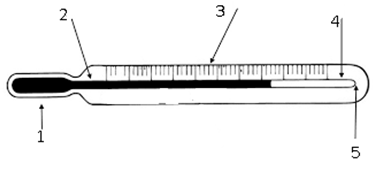
Pontos de fusão e ebulição da água
A escala Fahrenheit foi então redefinida com base nos pontos de fusão e de ebulição da água à pressão atmosférica como os novos pontos fixos. A fim de fazer a escala reformulada compatível com a antiga, os novos pontos foram definidos como sendo em 32 graus e a ebulição em 212 graus. Hoje essa escala de temperatura é chamada de escala de Fahrenheit (°F) e é amplamente utilizada em países de língua inglesa, como Estados Unidos e Inglaterra.
Conversão Celsius-Fahrenheit e Fahrenheit-Celsius
As escalas Celsius e Fahrenheit são utilizadas em porções distintas do globo, de forma que conversões de temperaturas tomadas entre ambas são algo bastante corriqueiro. Para efetuar as conversões entre as duas escalas, basta atentar para os pontos de fusão e de ebulição da água entre uma e outra.
Publicidade

Segundo a marcação da escala Fahrenheit, a água congela a 32 °F e entra em ebulição a 212 °F, de forma que há um intervalo de 180 graus entre ambos os pontos. Já na escala Celsius, os mesmos pontos coincidem o 0° e os 100°. Dessa forma, conclui-se cada intervalo de 1° F corresponde a uma fração de 5/9 da escala Celsius. Além disso, há uma intersecção das duas escalas nos 40 graus negativos. Dessa forma, para as conversões Celsius-Fahrenheit e Fahrenheit-Celsius, basta utilizar a seguinte equação de proporcionalidade:
ΔTC = ΔTF
5 9
Publicidade
Referências
EISBERG, R. M. and LERNER, L. S., Physics: Foundations and Applications, McGraw-Hill, 1981.

Por Carlos Ferreira
Formado em Ciências Econômicas e Jornalismo. Possui ampla experiência editorial e redacional em conteúdos jornalísticos com foco em mídias digitais.
Ferreira, Carlos. Grau Fahrenheit. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/a-escala-fahrenheit. Acesso em: 11 de July de 2025.
1. (ITA/95) O verão de 1994 foi particularmente quente nos Estados Unidos da América. A diferença entre a máxima temperatura do verão e a mínima do inverno anterior foi de 60ºC. Qual o valor dessa diferença na escala Fahrenheit?a) 33ºF
b) 60ºF
c) 92ºF
d) 108ºF
e) 140ºF
2. De forma sucinta como pode se pode criar uma escala de temperatura?
1. [d]
Para fazer a conversão da escala Celsius para a escala Fahrenheit, há que se utilizar a seguinte fórmula:
ΔTC = ΔTF
5 9
Ao substituir os 60°C da equação acima, temos
60 = ΔTF
5 9
12 = ΔTF
9
ΔTF = 12.9
ΔTF = 108 °F
2. Basta tomar dois fenômenos que acreditamos ocorrer sempre à mesma temperatura, depois fazer a escala do termômetro e posteriormente dividir a distância entre as duas marcas num número conveniente de intervalos iguais e igualmente espaçados. Cada uma delas representa um grau (°) na escala de temperaturas.