Histórico
“O termo logaritmo (logarithmus) foi criado por Napier e é formado pela junção das palavras gregas lógos e arithmós, que significam razão e número, respectivamente.” (IEZZI, et al. 1997)
Publicidade
O conceito de logaritmo foi inicialmente elaborado por John Napier, a partir de estudos relacionados à geometria no ano de 1614, quando foi publicada a primeira tábua de logaritmos. Paralelamente, Jobst Burgi conduziu seus estudos, embora apenas tenha publicado a tábua de logartimos resultante – baseada em noções algébricas – em 1620. A essa altura, o trabalho de Napier já estava difundido por toda Europa, mas ainda assim Burgi teve uma importante contribuição para a formalização do logaritmo.
O conceito de logaritmo de Napier e Burgi utilizava a base 1/e, sendo que e (o número de Euler) é um número irracional de valor aproximado de 2,718. O número de Euler é a base para definição dos logaritmos ditos naturais. Deste modo, o logaritmo natural, ou neperiano, ainda apresentava certas dificuldades de cálculo por usar a base 1/e, pois para se obter os logaritmos era necessário ter tabelas de consulta, chamadas tábuas de cálculo.

Posteriormente, Henry Briggs adaptou os logaritmos a uma base decimal.
Conceito
Os logaritmos criados a partir dos estudos de John Napier e Jobst Burgi, e posteriormente adaptados por Henry Briggs, possuem, atualmente, a seguinte lei de formação:
logab = x, onde:
a = base do logaritmo
Publicidade
b = logaritmando
x = logaritmo
A formulação atual de logaritmo foi estruturada por Leonhard Euler, no século XVIII, e relaciona logaritmo com a função exponencial. Nesse conceito, o logaritmo de um número b em uma base a é o expoente x que se deve aplicar à base de tal forma que o resultado seja b. Dessa forma:
Publicidade
logab = x ↔ ax = b, desde que a e b sejam números reais positivos (a ≠ 1, b > 0 e a > 0)
Em um exemplo:
Se:
log39 = x
Então:
3x=9
Ao fatorar o logaritmando 9 temos que:
9 = 3 X 3 = 32
Assim:
3x=9=32
3x=32
x=2
Sendo que:
a = 3 = base
b = 9 = logaritmando
x = 2 = logaritmo
Antilogaritmo
É definido como o inverso do logaritmo.
Exemplo:
antilog52=x
Primeiro, devemos igualar o antilogaritmo a x, que é o valor ao qual queremos chegar.
Em seguida, apenas aplicamos a definição dada acima:
5² = x
Facilmente podemos chegar ao valor de x apenas resolvendo a potência:
x = 5 * 5 = 25
Consequências da definição
A seguir, são apresentadas algumas propriedades que decorrem da definição de Briggs para logaritmos:
O logaritmo do número 1 em qualquer base sempre será igual a 0.
loga1 = 0, pois a0 = 1
O logaritmo de qualquer número a na própria base a será igual a 1.
logaa = 1, pois a1 = a
O logaritmo de uma potência da base é o expoente, em qualquer base.
logaam = m, pois m * logaa = m * 1 = m
A potência de base a e expoente logab é igual a b.
alogab = b, pois logab = x → ax = b
Com relação ao valor da base, o logaritmo da base 10 (b = 10) é chamado de logaritmo comum (ou decimal), sendo muito utilizado na ciência e engenharia. Ao trabalharmos com logaritmos na base 10 normalmente a omitimos.
O logaritmo natural (ou neperiano) tem a constante irracional e (≈ 2.718) como base e é utilizado na matemática pura, principalmente em cálculo diferencial. O nome neperiano é em homenagem a John Napier, autor do primeiro trabalho publicado que sintetizava a teoria dos logaritmos.
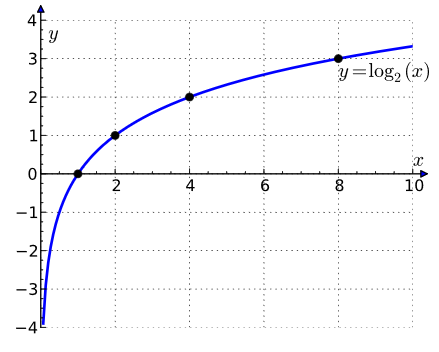
Por fim, há o logaritmo binário, no qual é utilizada a base 2 (b = 2), sendo de suma importância para a ciência da computação.
Propriedades dos logaritmos
As propriedades a seguir facilitam o uso de logaritmos em cálculos, uma vez que nos permitem obter o logaritmo de um produto, de um quociente ou de uma potência, sendo necessário conhecer apenas os logaritmos dos termos do produto, dos termos do quociente ou da base de potência.
Logaritmo do produto
“Em qualquer base a (0 < a ≠ 1), o logaritmo do produto de tais fatores reais positivos e igual à soma dos logaritmos dos fatores.” (IEZZI, et al. 1997)
Se:
0 < a ≠ 1, b > 0 e c > 0
Então:
loga (b . c) = loga b + loga c
Logaritmo do quociente
“Em qualquer base a (0 < a ≠ 1), o logaritmo do quociente de dois números reais positivos e igual a diferença entre o logaritmo do dividendo e 0 logaritmo do divisor.” (IEZZI, et al. 1997)
Se:
0 < a ≠ 1, b > 0 e c > 0
Então:
loga (b/c) = loga b – loga c
Logaritmo da potência
“Em qualquer base a (0 < a “* 1), o logaritmo de uma potencia de base real positiva e expoente real e igual ao produto do expoente pelo logaritmo da base da potência.” (IEZZI, et al. 1997)
Se:
0 < a ≠1, b > 0 e a Î IR
Então:
loga bα = α . loga b
Cologaritmo
É definido como o número real oposto de seu respectivo logaritmo.
Se:
0 < a ≠1, b > 0
Então:
colog ab = – logab
Mudança de base
Para realizar as propriedades operatórias, dois logaritmos de bases diferentes precisam ser convertidos para uma única base. No caso, se a, b e c são números reais positivos e a e c diferentes de 1, então:
loga b = logcb/logca
Exemplo:
log3 5 convertido para a base 2 fica
log3 5 = log2 5/log2 3
Referências
IEZZI, G.; DOLCE, O.; MURAKAMI, C. Fundamentos de matemática elementar 2: Logaritmos. 3.ed. São Paulo: Atual, 1997.
SEED-PR. Matemática / vários autores. Curitiba: SEED-PR, 2006.

Por Carlos Ferreira
Formado em Ciências Econômicas e Jornalismo. Possui ampla experiência editorial e redacional em conteúdos jornalísticos com foco em mídias digitais.
Ferreira, Carlos. Logaritmos. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/logaritmos. Acesso em: 03 de April de 2025.
1. [UFRGS/ 2011] Sabendo que log a = L e log b = M, então o logaritmo de a na base b é:
a) L + M
b) L – M
c) L.M
d) M/L
e) L/M
2. [PUCRJ/2003] Os valores de x tais que o logaritmo de 2x2 + 1 na base 10 é igual a 1 são:
(A) 1 e -1
(B) 1/√2 e -1/√2
(C) 3 e -3
(D) 3/√2 e -3/√2
(E) 1 e -2
1. [e]
Solução:
É pedido o logaritmo de a na base b, ou seja:
logba
Aplicando a fórmula da mudança de base:
logba = log10a / log10b
Relembre que este valor encontrado foi dado anteriormente no enunciado, portanto:
logba = L / M
2. [d]
Solução:
log y = 1, então y = 10
Logo:
2x2 + 1 = 10
2x2 = 9
x = +3√2 ou -3√