Dentre as características de uma função, Podemos classificá-la como sendo sobrejetora ou injetora. Quando a função possui essas duas características ao mesmo tempo, ela é chamada de função bijetora.
Publicidade
Dessa forma, estudaremos um pouco mais sobre a função bijetora, seu gráfico, alguns exemplos e resolveremos também alguns exercícios sobre esse assunto.
O que é uma função bijetora
Antes de entrarmos no assunto da função bijetora, vamos entender um pouco mais sobre o que é um domínio e um contradomínio de uma função.
O domínio de uma função pode ser visto como conjunto de “saída”, ou seja, é o conjunto que define a função. Em contrapartida, contradomínio é o conjunto de “chegada”, ou seja, é o conjunto que contém todas as possíveis imagens da função.
.
Além disso, precisamos relembrar o que são as funções injetoras ou sobrejetoras antes de entendermos a função bijetora. Uma função injetora é aquela que os elementos de um conjunto domínio de uma função qualquer se relacionam com elementos distintos do contradomínio dessa função.
Uma função é considerada sobrejetora quando todo elemento do contradomínio é imagem de pelo menos um elemento do domínio dessa função. Dessa forma, uma função bijetora ocorre quando os elementos do domínio se relacionam com elementos distintos do contradomínio (função injetora) e ao mesmo tempo o contradomínio é imagem de um elemento do domínio (função sobrejetora).
Publicidade
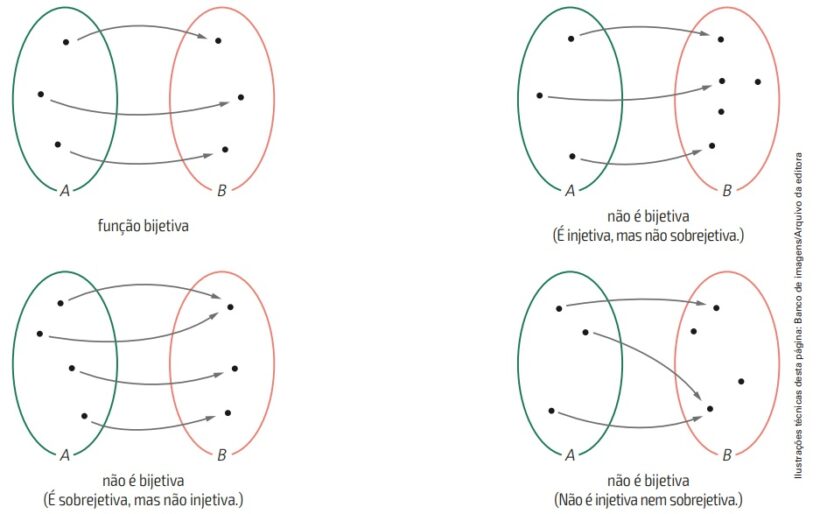
Na imagem acima é possível ver três exemplos de funções não bijetora, porém, em alguns casos, elas são injetoras ou sobrejetoras. O único caso de função bijetora é o primeiro diagrama, onde se observa que o domínio se relaciona com apenas um elemento do contradomínio e o contradomínio é imagem do domínio.
De uma maneira mais formal, podemos definir uma função bijetora da seguinte forma:
Publicidade
Uma função f: A → B é bijetora (bijetiva) se ela for, simultaneamente, injetora e sobrejetora. Quando isso ocorre dizemos que há uma bijeção ou uma correspondência biunívoca entre os conjuntos domínio A e contradomínio B.
Função Inversa
Quando uma função é bijetora, ela pode admitir uma inversa conhecida como função inversa. Essa função nada mais é do que a “troca” do domínio pelo contradomínio. Por exemplo, se uma função bijetora tem domínio A e contradomínio B, sua inversa terá domínio B e contradomínio A.
As funções inversas são importantes para o entendimento desse assunto, além de terem muitas aplicações na matemática.
Gráfico de uma função bijetora
Assim como funções sobrejetoras e injetoras possuem gráficos, a função bijetora também não seria diferente. Aqui entenderemos um pouco mais sobre o gráfico dessa função.
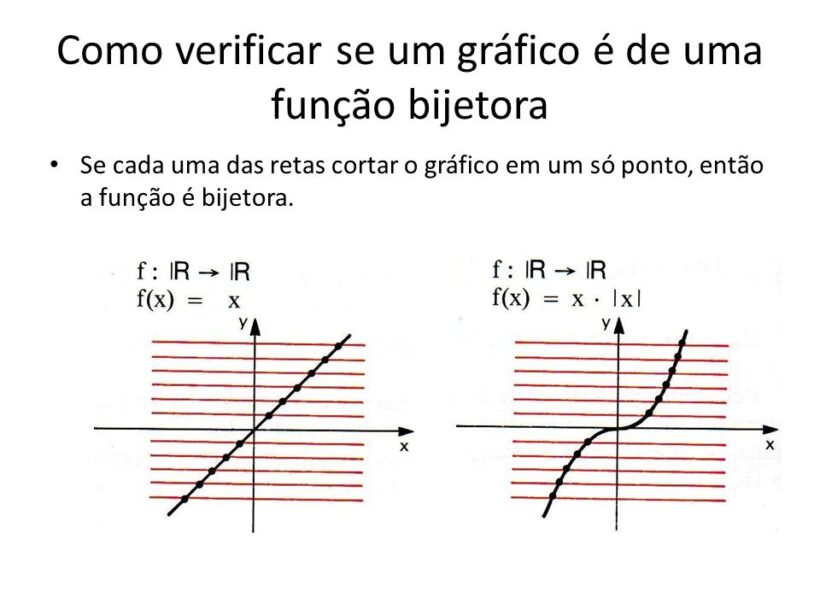
Nos gráficos acima, se traçarmos retas horizontais, essas retas tocaram em apenas um ponto, assim como na função injetora. Por outro lado, é possível observar que nos extremos do gráfico não existe um limite, ou seja, ele cresce ou decresce indefinidamente, assim como no gráfico de uma função sobrejetora.
O entendimento desse gráfico é de extrema importância, pois é muito fácil confundir com o gráfico de uma função injetora ou sobrejetora.
Exemplos de função bijetora
Vamos então entender alguns exemplos de função bijetora de tal forma que essas funções são representadas por uma fórmula matemática.
A função do triplo de um número
O triplo de um número pode ser definida como a seguinte função f(x) = 3x, ou ainda, f: R → R . Essa função é bijetora, pois existe apenas um valor triplo de um número qualquer do domínio de f(x). Além disso, todo número real possui um triplo.
Equação de uma reta simples
Seja uma dada reta definida pela função f: R → R tal que f(x) = x + 1. Essa função é bijetora pois cada número real do domínio R tem sempre um só correspondente no contradomínio R (esse número mais 1)
Existem muitos outros exemplos de função bijetora. Os exemplos nos ajudam a entender um pouco mais sobre a definição dessa função, assim como seu gráfico.
Entenda mais sobre função bijetora
Podemos utilizar os conteúdos em vídeo para explicações visuais de conteúdos. Vamos então aprender um pouco mais sobre função bijetora a partir dos vídeos que selecionamos seguir.
A função bijetora
Neste vídeo, é apresentada a definição da função bijetora, além de apresentar alguns exemplos e demonstrar os gráficos de funções bijetoras.
Uma breve explicação
Do mesmo modo, esse vídeo explica sobre a função bijetora, porém de uma maneira mais resumida.
Os vídeos são uma forma de nos aprofundarmos em determinado conteúdo, facilitando assim o nosso entendimento.
Funções bijetoras possuem muitas aplicabilidades na matemática, sendo importantes também para outras áreas como física e a química. Por isso é importante o conhecimento dessa função.
Referências
Matemática: ciência e aplicações – Gelson Iezzi;
Matemática: contexto & aplicações – Luiz Roberto Dante.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Função bijetora. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcao-bijetora. Acesso em: 04 de April de 2025.
1.
Defina a função abaixo e classifique-a em injetora, sobrejetora ou bijetora.
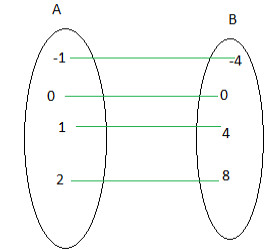
A função é definida por:
F(x) = 4x
Veja: 4 . (-1) = -4
4 . (0) = 0
4 . 1 = 4
4 . 2 = 8
A Função é injetora, pois os elementos distintos do domínio têm imagens distintas. Além disso, a função é sobrejetora pois o contradomínio é igual à imagem. Deste modo, a função é bijetora.
2.
Marque a alternativa que representa a função abaixo:
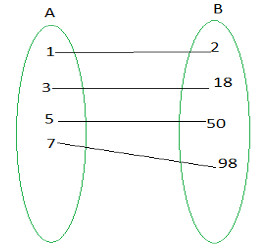
a) f(x) = 2x + 2; Bijetora
b) f(x) = x² + 2; Injetora
c) f(x) = 2x²; Sobrejetora
d) f(x) = 2x²; Bijetora
e) f(x) = x²; Injetora
A função é definida por F(x) = 2x²
Observe:
F(1) = 2.(1)² = 2
F(3) = 2.(3)² = 18
F(5) = 2.(5)² = 50
F(7) = 2.(7)² = 98
Funções que como essa são tanto sobrejetoras quanto injetoras, são classificadas como funções bijetoras.
RESPOSTA: d)