Funções trigonométricas

Em uma região litorânea, é possível se observar a famosa maré. Em resumo, é um evento que se repete em intervalos de tempos iguais. Esse é um exemplo de fenômeno periódico. Esses fenômenos podem ser descritos por meio de funções trigonométricas, assunto desta matéria. Entenda, a seguir, o que é uma função periódica, além de seu domínio, imagem e contradomínio.

Publicidade

O que são funções trigonométricas

No primeiro ano do ensino médio, a princípio, são estudados o seno, o cosseno e a tangente de um triângulo retângulo. Nesta seção vamos associar um número real a esses conceitos. Para realizar tal associação, utiliza-se a função seno, a função cosseno e a função tangente.

As funções seno e cosseno possuem os mesmas características em suas definições. Contudo, diferenciam-se em suas representações gráficas, que serão apresentadas mais adiante. Por outro lado, a função tangente tem certas limitações em seu domínio, pois ela não é definida, em certos pontos, no eixo dos números reais. Sua imagem, porém, abrange todos os números reais.

Funções periódicas

No cotidiano, encontram-se diversos fenômenos que se repetem em um mesmo intervalo de tempo. É dado o nome de período para o menor intervalo de tempo em que ocorre essa repetição.

Tais fenômenos podem ser descritos por funções periódicas. Pode-se, então, definir uma função periódica da seguinte maneira:

Uma função f: A ⟶ B é periódica se existir um número real positivo p tal que f(x) = f(x + p), ∀ xϵA. O menor valor positivo de p é chamado de período de f.

Publicidade

Função seno

Seja x um número real e P, sua imagem na circunferência trigonométrica. Assim, a função seno é uma função definida como f:R ⟶R que associa cada número real x a seu seno, ou seja, f(x) = sen(x).

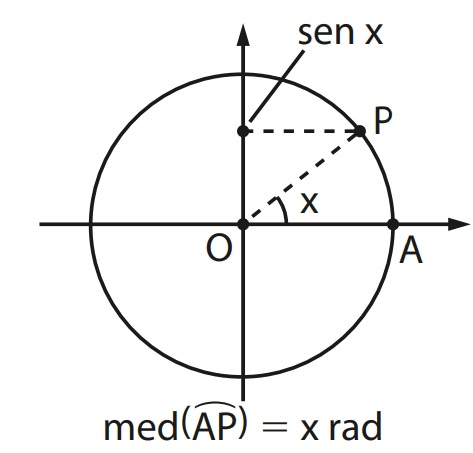
Na imagem, podemos observar que a função seno é periódica, tendo seu domínio em todos os número reais e sua imagem podendo ser apenas de -1 até 1.

Publicidade

A função seno troca seu sinal (positivo ou negativo) dependendo da região onde está. Ela é positiva no 1° e no 2° quadrantes e negativa no 3° e no 4° quadrantes.

Além disso, a função seno tem período igual a 2π. Ela é conhecida também como sendo uma função ímpar, pois sen(-x) = -sen(x).

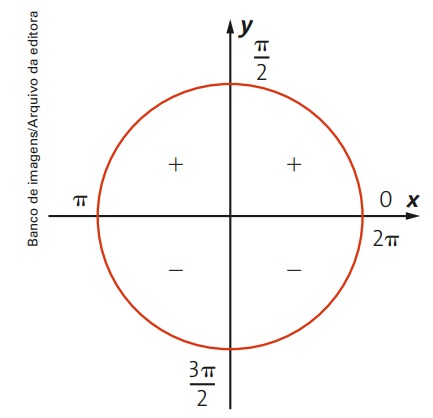
Gráfico da função seno

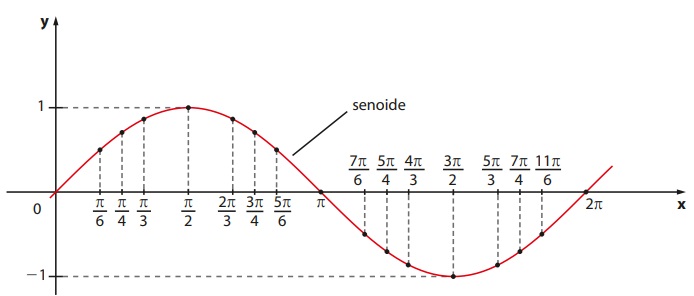
O gráfico da função seno recebe o nome de senoide. A imagem representa apenas um período da função seno, pois, como ela é periódica, essa representação se repetirá durante todo o domínio.

Função cosseno

Seja x um número real e P, sua imagem na circunferência trigonométrica. Dessa forma, a função cosseno é uma função definida como f:R ⟶R que associa cada número real x a seu cosseno, ou seja, f(x) = cos(x).

Diferentemente da função seno, a função cosseno associa a cada número real x o eixo das abcissas do ponto correspondente à sua imagem P.

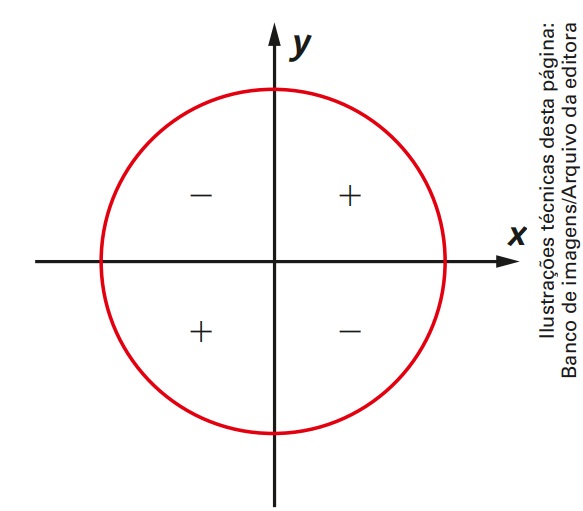
Assim como na função seno, existe também uma alternância no sinal da função cosseno. No 1° e no 4° quadrantes, a função cosseno é positiva. Já no 2° e no 3° quadrantes, ela é negativa.

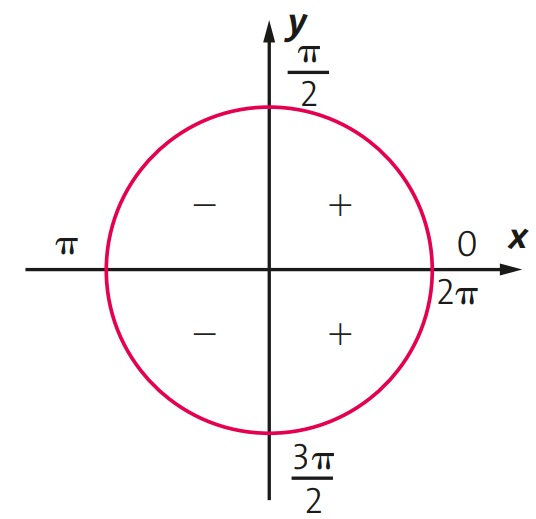
Por fim, a função cosseno é uma função par, pois cos(-x) = cos(x). Seu período é o mesmo da função seno, ou seja, 2π.

Gráfico da função cosseno

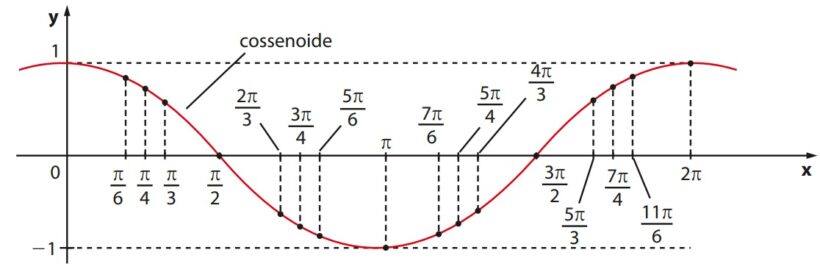
O gráfico da função cosseno, representado na figura anterior, é conhecido como cossenoide. Ele é quase idêntico ao gráfico da função seno, tendo apenas a diferença de estar defasado em π/2.

Função tangente

A função tangente é definida como sendo uma função f tal que f: {x ∈ R│x ≠ de π/2 + kπ; K ∈ Z} ⟶R, ou seja, temos que f(x) = tan(x).

Podemos observar que existe uma certa limitação para o domínio da função tangente, ou seja, ela não é definida para certos valores de x.

Assim como nas outras funções, o sinal da função tangente também varia no círculo trigonométrico. No 1° e no 3° quadrantes, a função tangente é positiva. Por outro lado, no 2° e no 4° quadrantes, ela é negativa.

O período da função tangente é π. Por fim, essa função é definida como uma função ímpar, pois tan(-x) = -tan(x).

Gráfico da função tangente

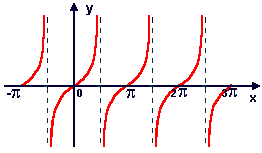
No gráfico acima, podemos observar algumas retas verticais, que são chamadas de assíndotas verticais. Elas recebem esse nome devido ao fato de que, nos pontos por onde elas passam, não existe ponto em comum com o gráfico.

Entenda mais sobre funções trigonométricas

A seguir, há uma selação de vídeos explicativos que podem te auxiliar no entendimento desse assunto. Confira:

Função seno

Nesse vídeo, é possível entender um pouco mais sobre a definição de uma função seno.

Função cosseno

Da mesma forma, nesse vídeo, você verá um aprofundamento maior sobre a função cosseno, suas definições e seu gráfico.

As funções trigonométricas são muito importantes para os estudos de matemática, pois são necessárias em alguns exemplos práticos do dia a dia. Para continuar seus estudos de trigonometria, que tal aprender também sobre a classificação dos triângulos?

Referências