Sejam f e g funções. Podemos, então, escrever uma função h que possa ser uma combinação das funções. Chamamos isso de composição de função ou simplesmente função composta.
Publicidade
Por outro lado, devemos ter o conhecimento sobre o conceito das funções inversas. Isso se deve ao fato de que essas podem ser confundidas com funções compostas. Dessa maneira, vamos identificar a diferença entre elas.
Definição
Frequentemente, definimos uma função composta da seguinte maneira:
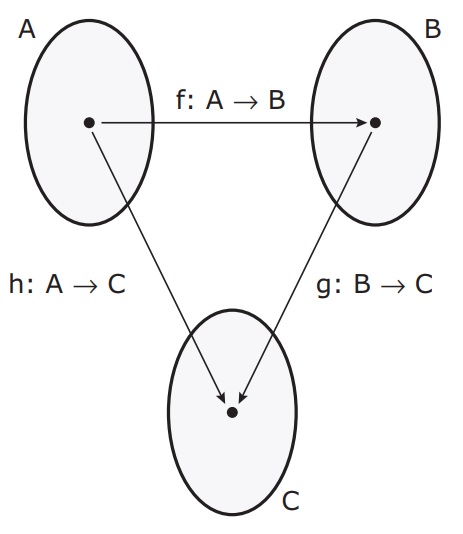
Sejam A, B e C conjuntos e sejam as funções f: A -> B e g: B -> C. A função h: A -> C tal que h(x) = g(f(x)) é chamada de função composta de g com f. Indicaremos essa composição por g o f, lê-se “g composta f”.
Relacionadas
Alguns exemplos de função composta
A área de um terreno
Vamos considerar, a princípio, o seguinte exemplo. Um terreno foi dividido em 20 lotes. Todos os lotes são quadrados e áreas iguais.
De acordo com o que foi apresentado, vamos mostrar que a área do terreno é uma função da medida do lado de cada lote, representando, assim, uma função composta.
Antes de mais nada, vamos indicar o que é cada uma das informações necessárias. Dessa forma, temos:
- x = medida do lado de cada lote;
- y = área de cada lote;
- z = área do terreno.
Sabemos que o lado da figura geométrica do quadrado é o valor do lado desse quadrado elevado ao quadrado.
Publicidade
De acordo com o enunciado do exemplo, obtemos que a área de cada lote é uma função da medida do lado, segundo a imagem a seguir:
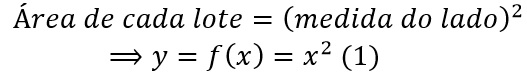
Do mesmo modo, a área do terreno total pode ser expresso, como uma função de cada, ou seja:
Publicidade
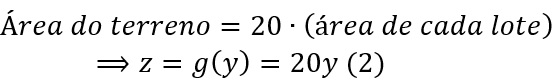
Para mostrarmos o que se pede, de antemão, vamos “substituir” a equação (1) na equação (2), assim:
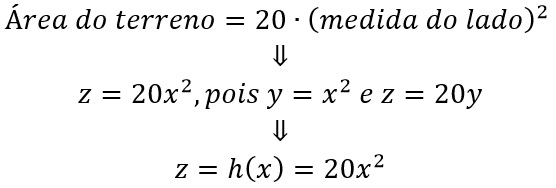
Em conclusão, podemos afirmar que a área do terreno é uma função da medida de cada lote.
Relação de duas expressões matemáticas
Suponha agora o seguinte esquema:
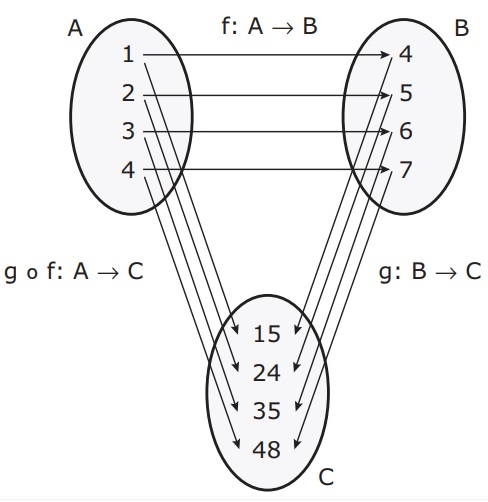
Sejam f:A⟶B e g:B⟶C funções que são definidas da seguinte maneira:
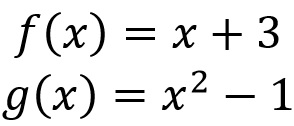
Por outro lado, vamos identificar a função composta g(f(x)) que relacionam os elementos do conjunto A com o conjunto C.
Para fazermos isso, antecipadamente, precisamos apenas “colocar” a função f(x) dentro da função g(x), conforme segue abaixo.
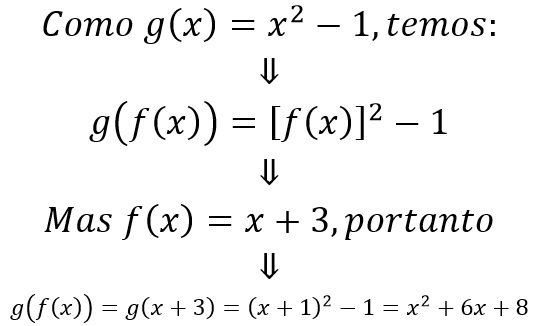
Em síntese, podemos observar a seguinte situação:
- Para x = 1, temos g(f(1)) = 12 + 6.1 + 8 = 15
- Para x = 2, temos g(f(2)) = 22 + 6.2 + 8 = 24
- Para x = 3, temos g(f(3)) = 32 + 6.3 + 8 = 35
- Para x = 4, temos g(f(4)) = 42 + 6.4 + 8 = 48
Enfim, a expressão g(f(x)) realmente relaciona os elementos do conjunto A com os elementos do conjunto C.
Função composta e função inversa
Definição de função inversa
Primeiramente, vamos relembrar a definição de uma função inversa, em seguida, entenderemos a diferença entre função inversa e função composta.
Dada uma função f: A → B, bijetora, denomina-se função inversa de f a função g: B → A tal que, se f(a) = b, então g(b) = a, com aϵA e bϵB.
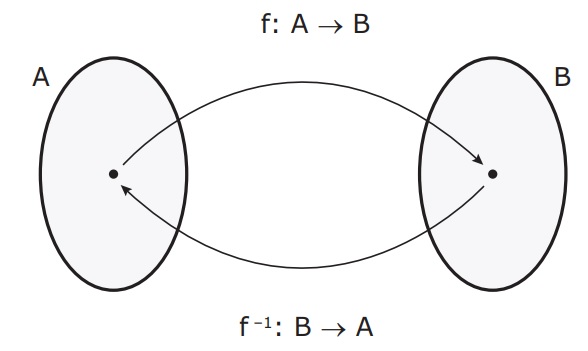
Em suma, uma função inversa nada mais é do que uma função que “reverte” o que foi feito.
Diferença entre função composta e função inversa
A princípio, pode ser difícil observar qual é a diferença entre as duas funções.
A diferença existe justamente nos conjuntos de cada função.
Uma função composta leva um elemento de um conjunto A diretamente até um elemento do conjunto C, pulando o conjunto B no meio do caminho.
Porém, a função inversa apenas pega um elemento de um conjunto A, leva até o conjunto B e depois faz o contrário, ou seja, pega esse elemento de B e leva até A.
Dessa forma, podemos observar que a diferença entre as duas funções está na operação que realizam.
Aprenda mais sobre função composta
Para entender melhor, selecionamos alguns vídeos com explicações sobre o tema.
Função composta, sua definição e exemplos
Este vídeo apresenta a definição de função composta e de alguns exemplos.
Mais exemplos de função composta
Alguns exemplos a mais sempre são bem vindos. Este vídeo apresenta e soluciona outras funções compostas.
Um exemplo de função inversa
Nesse vídeo, podemos entender um pouco mais sobre a função inversa com uma explicação passo a passo.
A função composta, é muito utilizada em vários vestibulares, sendo assim a essencial compreensão desse assunto para quem vai fazer a prova.
Referências
Colégio Bernoulli, Matemática: volume 3;
Manoel Paiva, Matemática;
Luiz Roberto Dante, Matemática: contexto & aplicações..

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Função Composta. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/funcao-composta. Acesso em: 03 de April de 2025.
1. [BRDE 2012]
Seja f: R+ → R dada por f(x) = √x e g: R → R+ dada por g(x) = x² + 1. A função composta (g o f)(x) é dada
a) √x² + 1
b) x+1
c) √x² + 1
d) √x²
e) x² + 1
Como queremos (g o f)(x), ou g(f(x)), precisamos apenas substituir a função f(x) em g(x), assim
g(f(x)) = f(x)2 + 1
Como f(x) = √x, temos que
g(f(x)) = (√x)2 + 1
Portanto
g(f(x)) = x + 1
A resposta correta é a letra b.
2. [Mackenzie – SP]
As funções f(x) = 3–4x e g(x) = 3x+m são tais que f(g(x)) = g(f(x)), qualquer que seja x real. O valor de m é:
a) 9/4
b) 5/4
c) –6/5
d) 9/5
e) –2/3
Sabendo que f(g(x)) = g(f(x)):
Vamos realizar a composição de funções de ambos os lados da igualdade:
3 – 4.(3x+m) = 3.(3-4x) + m
3-12x-4m = 9-12x+m
-4m-m = 9-3-12x+12x
-5m = 6
(-1).-5m = 6.(-1)
5m = -6
m = – 6/5
Portanto, para que a igualdade f(g(x)) = g(f(x)) seja verdadeira, é necessário que m = – 6/5.
A resposta correta é a letra c.
3. [PUC - PR]
Considere f(x) = (x2 – 1)/(x – 2) e g(x) = (x – 1) e . Calcule f(g(x)) para x = 4:
a) 6
b) 8
c) 2
d) 1
e) 4
Vamos realizar a composição de f(g(x)):
f(g(x)) = [(x-1)2-1]/[(x-1)-2]
f(g(x)) = (x2 -2x+1-1)/(x-1-2)
f(g(x)) = (x2-2x)/(x-3)
Agora que realizamos a composição de funções, vamos substituir x = 4 na função que encontramos:
f(g(4)) = (42-2.4)/(4-3)
f(g(4)) = (16-8)/1
f(g(4)) = 8
Portanto, a composição f(g(x)), quando x = 4, é 8.
A resposta correta é a letra b.
4. [Cefet – PR]
Se f(x) = x5 e g(x) = (x – 1), a função composta f[g(x)] será igual a:
a) x5 + x – 1
b) x6 – x5
c) x6 – 5x5 + 10x4 – 10x3 + 5x2 – 5x + 1
d) x5 – 5x4 + 10x3 – 10x2 + 5x – 1
e) x5 – 5x4 – 10x3 – 10x2 – 5x – 1
Sendo f(x) = x5 e g(x) = x – 1, vamos realizar a composição de funções f[g(x)], isto é, onde houver x na função f(x), nós substituiremos por g(x) = x – 1:
f(x) = x5
f(g(x)) = [g(x)]5
f(g(x)) = [x – 1]5
f(g(x)) = (x – 1)².(x – 1)².(x – 1)
f(g(x)) = (x² – 2x + 1) . (x² – 2x + 1) . (x – 1)
f(g(x)) = (x4 – 2x³ + x² – 2x³ + 4x² – 2x + x² – 2x + 1) . (x – 1)
f(g(x)) = (x4 – 4x³ + 6x² – 4x + 1) . (x – 1)
f(g(x)) = x5 – 4x4 + 6x³ – 4x² + x – x4 + 4x³ – 6x² + 4x – 1
Portanto, a função composta é
f(g(x)) = x5 – 5x4 + 10x³ – 10x² + 5x – 1
A resposta correta é d.