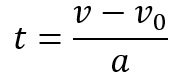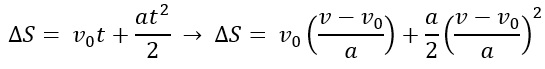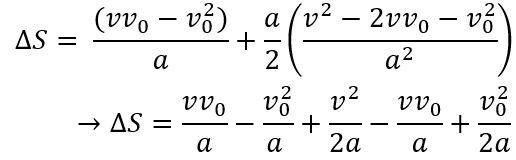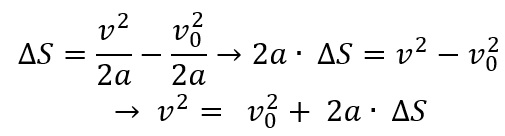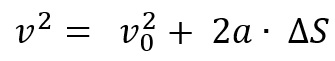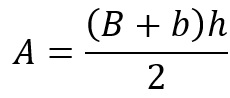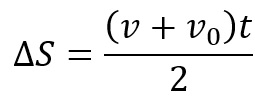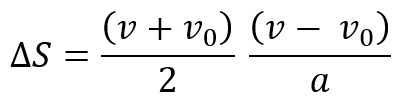Existem três equações para o movimento uniformemente variado. Uma delas é conhecida como equação de Torricelli. Em suma, essa equação evita muitos cálculos em alguns tipos de exercícios.
Publicidade
Juntamente com as outras equações, demonstraremos como obteremos a equação de Torricelli. Da mesma forma, conheceremos um pouco da história de Torricelli e em quais situações aplicar a equação que leva seu nome.
Quem foi Evangelista Torricelli?

Evangelista Torricelli nasceu em Florença no dia 15 de outubro de 1608 e faleceu no dia 25 de outubro 1647, na cidade onde nasceu.
Relacionadas
Ele foi o irmão mais velho dos três filhos de Gaspare Torricelli e Catarina Torricelli.
Torricelli realizou seus estudos matemáticos em diversas instituições jesuítas e também teve contato com estudos de vários filósofos naturais.
Além de seus tratados e descobertas matemáticas, Torricelli foi o inventor barômetro de mercúrio. Em 1644, publicou sua obra mais conhecida: Ópera Geométrica.
O que é a equação de Torricelli
Em síntese, a equação de Torricelli é derivada das funções horárias do tempo do movimento uniformemente variado. Dessa forma, ela foi desenvolvida pela necessidade da independência temporal das equações do M.R.U.V. Ela é utilizada principalmente em exercícios que não consideram a variável tempo. Logo, ela facilita muito os cálculos.
Publicidade
A fórmula da equação de Torricelli
Antes de mais nada, vamos ver como obter a equação de Torricelli.
Vamos, primeiro, isolar a variável tempo na equação v = v0 + at . Obtemos, então, a seguinte equação para o tempo:

Publicidade
Substituindo essa expressão na função horária do deslocamento, logo, obtemos que:
Dessa forma, vamos “abrir” a expressão acima:
Então, vamos isolar v para chegarmos na equação de Torricelli.
Portanto, a fórmula de Torricelli é:
Dessa forma, os elementos da equação são:
- v: velocidade final do objeto;
- v0: velocidade inicial do objeto;
- a: aceleração do objeto;
- ∆S: deslocamento escalar realizado pelo objeto.
Assim, com a equação estabelecida, podemos prosseguir para a aplicação em alguns exercícios e o aprimoramento da equação.
Gráfico da equação de Torricelli

A princípio, o gráfico da equação de Torricelli são os que relacionam a velocidade com o tempo, ou seja, formam uma reta, conforme observamos no gráfico acima.
O espaço percorrido pelo móvel pode ser obtido pela área do gráfico da velocidade pelo tempo. Segundo o gráfico, a área corresponde a de um trapézio, assim:
Em que B é a base maior, b é a base menor do trapézio e h é a altura. Substituindo os valores do gráfico na equação da área, obtemos:
Por outro lado, sabemos que:
Dessa forma, o cálculo do deslocamento, conforme o gráfico da velocidade por tempo, fica:
Em conclusão, aplicando as regras da distributiva na expressão acima, podemos obter a equação de Torricelli a partir do gráfico de velocidade por tempo do M.R.U.V.
Entenda mais sobre equação de Torricelli
Agora você já entende o básico sobre a fórmula de Torricelli, assista aos vídeos abaixo e complemente seus estudos com deduções detalhadas e exemplos de aplicação:
Demonstração da equação de Torricelli
Neste vídeo, definitivamente, podemos ver como é obtido a equação estudada no texto e uma aplicação em um exercício.
Aplicando a equação de Torricelli em um exercício de vestibular
Do mesmo modo, esse vídeo mostra a aplicação da equação em um exercício voltado para o vestibular.
Aplicando Torricelli em vários exercícios de vestibular
Para fixar o conteúdo, em conclusão, esse vídeo mostra a resolução de vários exercícios utilizando a fórmula de Torricelli.
Referências
Kazuhito Yamamoto, Física para o ensino médio, vol. 1 : mecânica;
Wilson Carron, As faces da física : volume único.

Por Guilherme Santana da Silva
Graduado no curso de Física pela Universidade Estadual de Maringá. Professor assistente em um colégio de ensino médio e preparatório para os vestibulares. Nas horas vagas se dedica à vida religiosa, praticar mountain bike, tocar bateria, dar atenção à família e cuidar de suas duas gatinhas Penélope e Mel.
Santana, Guilherme. Equação de Torricelli. Todo Estudo. Disponível em: https://www.todoestudo.com.br/fisica/equacao-de-torricelli. Acesso em: 03 de April de 2025.
1. [FPS-PE]
Um automóvel percorre uma rodovia com velocidade inicialmente constante igual a 80 km/h. O motorista do veículo avista um radar e reduz sua velocidade para 60 km/h, percorrendo nesse trajeto uma distância igual a 20 m. O módulo da desaceleração sofrida pelo automóvel nesse percurso foi de aproximadamente:
a) 5,4 m/s2
b) 7,5 m/s2
c) 2,5 m/s2
d) 11 m/s2
e) 15 m/s2
O tempo percorrido pelo automóvel não foi fornecido. Assim, iremos utilizar a equação de Torricelli.
Dados:
v0 = 80km/h = 22m/s (velocidade inicial)
v = 60km/h = 16m/s (velocidade final)
ΔS = 20m (espaço de frenagem)
Utilizando então a equação de Torricelli, temos que:

Como é uma desaceleração, o sinal negativo na aceleração demonstra isso.
RESPOSTA: a) (Pois é um valor aproximado)
2. [UERN]
Um automóvel que se encontrava em repouso entra em movimento retilíneo uniformemente variado atingindo em 20 s uma velocidade de 90 km/h. A partir de então ele mantém essa velocidade por mais 20 s e, em seguida, passa a desacelerar gastando também 20 s para voltar ao repouso. A distância percorrida por esse automóvel em todo o percurso é:
a) 0,5 km.
b) 1 km.
c) 1,5 km.
d) 2 km.
A determinação da distância total percorrida pelo móvel será feita em três etapas.
Dados: 90 km/h = 25 m/s
1 – Aceleração durante os 20 s iniciais.
Primeiramente, deve-se determinar a aceleração do móvel a partir da função horária da velocidade para o movimento retilíneo uniformemente variado.
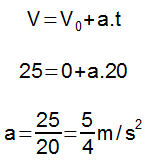
A partir da equação de Torricelli, o espaço percorrido durante a aceleração poderá ser determinado.
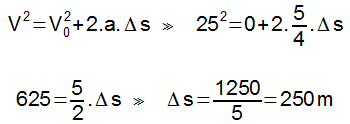
2 – Espaço percorrido durante os 20 s com velocidade constante.
Durante o período de velocidade constante, o espaço percorrido será definido pela função horária da posição para o movimento retilíneo uniforme.
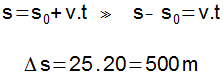
3 – Desaceleração durante os 20 s.
A desaceleração é feita nas mesmas condições da aceleração, logo, em módulo, os valores são os mesmos. Assim, o espaço necessário para parar é exatamente igual ao espaço da aceleração, ou seja, 250 m.
Somando os resultados obtidos nas três etapas, o deslocamento total do automóvel é de 1000 m ou 1 km.
RESPOSTA: b)