A equação quadrática, ou equação de segundo grau, é uma equação polinomial de grau dois, e é representada do seguinte modo:
Publicidade
ax2+bx+c=0
Onde:
- x é uma variável, cujo valor deve ser determinado; e
- a, b e c são constantes.
O termo a é o coeficiente quadrático, o b o coeficiente linear e c o termo livre. Para ser uma equação quadrática, a ≠ 0. Caso contrário, a equação será uma equação linear.
Uma equação de segundo grau pode ter até duas soluções, chamadas de raízes da equação, que são obtidas pela seguinte fórmula geral:
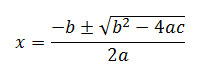
Sendo que o discriminante da equação é o valor de:
Publicidade
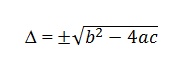
O discriminante da equação determina o número e a natureza das raízes e pode ser:
- ∆ > 0, a equação tem duas raízes reais diferentes
- ∆ = 0, a equação tem duas raízes reais iguais
- ∆ ˂ 0, a equação não tem raízes reais
Internacionalmente não existe a nomenclatura “fórmula de Bhaskara”. Esta denominação é utilizada somente no Brasil e inadequadamente, pois Bhaskara Acharya nasceu em 1.114 na Índia, no entanto referências sobre a fórmula de Bhaskara estão presentes em textos babilônicos de mais de 4.000 anos.
Publicidade
Geometria
As raízes da equação quadrática, são também as raízes da função quadrática:
f(x) = ax2+bx+c
Então, se os termos a, b, e c são números reais e o domínio de f é o conjunto dos números reais, então as raízes de f são as abcissas dos pontos nos quais o gráfico toca o eixo x. Assim, se o discriminante é positivo, o gráfico toca o eixo x em dois pontos, se for zero o gráfico toca em apenas um ponto e se for negativo, o gráfico não encosta no eixo x.
Sentido da parábola
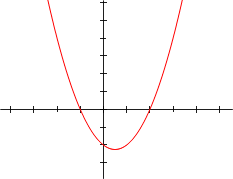
O valor do termo a indica a característica e direção da Parábola.Se a for igual a zero, a equação é linear, não existe uma parábola, e sim uma reta bx + c. Se a for positivo, a parábola terá o aspecto de U. Se a for negativo, a parábola terá o aspecto de ∩.
Você sabia?
Quem foi Bhaskara?
Bhaskara Akaria foi um matemático, professor, astrólogo e astrônomo indiano. Considerado o mais importante matemático do século XII, Bhaskara nasceu em uma tradicional família de astrólogos indianos. Escreveu o “Bijaganita”, livro sobre álgebra que o tornou famoso como matemático. No entanto, Bhaskara não foi o descobridor da fórmula que leva seu nome, já que tais fórmulas só surgiram cerca de 400 anos após sua morte.

“O nome de Bhaskara dado à resolução da equação do segundo grau estabeleceu-se, no Brasil, por volta de 1960. Essa equação é tratada em outros países como fórmula geral para resolução da equação polinomial do segundo grau, estratégia essa conhecida há mais de quatro mil anos pelos babilônicos.”
(Refatti & Bisognin, 2005)
Referências
BOYER, C. B. História da Matemática. São Paulo, Edgar Blucher, 1974.
REFATTI, L. R.; BISOGNIN, E. Aspectos Históricos e Geométricos da Equação Quadrática. Disc. Scientia. Série: Ciências Naturais e Tecnológicas, Santa Maria, v. 6, n. 1, p.79-95, 2005.

Por Carlos Ferreira
Formado em Ciências Econômicas e Jornalismo. Possui ampla experiência editorial e redacional em conteúdos jornalísticos com foco em mídias digitais.
Ferreira, Carlos. Fórmula de Bhaskara. Todo Estudo. Disponível em: https://www.todoestudo.com.br/matematica/formula-de-bhaskara. Acesso em: 06 de January de 2026.
1. (PUCCAMP/2013) Se v e w são as raízes da equação x2 + ax + b = 0, em que a e b são coeficientes reais, então v2 + w2 é igual a:
a) a2 – 2b
b) a2 + 2b
c) a2 – 2b2
d) a2 + 2b2
e) a2 – b2
2. (UEL/98) A soma de um número racional não inteiro com o dobro do seu inverso multiplicativo é 33/4. Esse número está compreendido entre:
a) 5 e 6
b) 1 e 5
c) 1/2 e 1
d) 3/10 e 1/2
e) 0 e 3/10
1. [a]
Identificando os coeficientes da equação:
A = 1, B = a e C = b.
Agora basta aplicar esses valores na fórmula de Bhaskara. Para não nos confundirmos, neste exercício utilizaremos letras maiúsculas na fórmula de Bhaskara. Ao substituir os coeficientes, utilizaremos letras minúsculas como de costume:
Δ= a2 – 4.1.b
Δ= a2 – 4.b
Essa equação terá duas raízes, o que as diferenciará será o sinal ± que antecede a raiz quadrada. Então, iremos considerar como v o resultado com a raiz quadrada positiva e como w o resultado com a raiz quadrada negativa. A soma dos quadrados de v e w é dada por:
v2 + w2
Como possuem sinais opostos, os dois termos com raiz serão cancelados, restando apenas:
(a² + a² – 4b + a² + a² – 4b)/4
(4a² – 8b)/4
a² – 2b
Portanto, a alternativa correta é a letra a.
2. [e]
Chamaremos por x o número que estamos procurando, seu inverso multiplicativo é 1/x. Se a soma de x com o dobro de seu inverso multiplicativo é 33/4, teremos:
(x + 2. 1)/x = 33/4
4x² + 8 = 33x
4x² – 33x + 8 = 0
Para resolvendo usando a fórmula de Bhaskara:
Δ = (– 33)² – 4.4.8
Δ= 1089 – 128
Δ= 961
x = [– (– 33) ± √961]/2.4
x = (33 ± 31)/8
x’ = 64/8 = 8
x” = 2/8 = 1/4
São encontradas duas raízes para a equação. Porém, o exercício refere-se apenas à raiz que é um número racional não inteiro. Portanto, o primeiro resultado não é interessante, sendo que 8 é um número inteiro.
Assim, utilizaremos o valor de x”, uma vez que ¼ = 0,25.
A alternativa correta é a letra e, pois ¼ é maior que zero e é menor que 3/10, que equivale a 0,3.